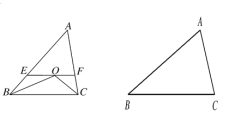
【题目】如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过O做EF∥BC分别交AB、AC于E、F.
(1)求证:EF=BE+CF.
(2)在△ABC中,∠ABC的角平分线与∠ACB相邻的外角的平分线相交于点O,过O做EF∥BC分别交AB、AC于E、F,请你画出图形(不要求尺规作图),并直接写出EF、BE、CF之间的关系.
参考答案:
【答案】(1)证明见解析;(2)作图见解析;EF=BE-CF
【解析】
(1)根据角平分线和平行线的性质分别证明∠EBO=∠EOB,∠FOC=∠FCO,从而得出EO=BE,FO=CF,即可解决问题;
(2)根据角平分线的额作法步骤,分别作出∠ABC和∠ACB的角平分线,两条角平分线的交点即为点O,
(1)证明:∵BO平分∠ABC,
∴∠EBO=∠OBC,
∵EF∥BC,
∴∠EOB=∠OBC,
∴∠EBO=∠EOB,
∴EO=BE,
同理:FO=CF,
∴EO+FO=BE+CF,
即EF=BE+CF.
(2)以点B为圆心,以任意长为半径作弧,分别交BA和BC与点M和点D;
分别以M和D为圆心,以大于MD的一半为半径作弧,交于点N,作射线BN,则射线BN即为∠ABC的角平分线;
同理作∠ACB外角的角平分线,两线交于点O,过点O作BC的平行线交AB与点E,交AC于点F.如图所示:
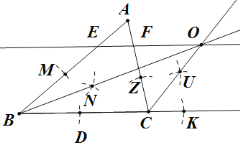
∵OE∥BC,
∴∠EOB=∠CBO,
∵BN是∠ABC的角平分线,
∴∠ABN=∠CBO,
∴∠ABN=∠EOB,
∴BE=OE,
∵OE∥BC,
∴∠OCK=∠FOC,
∵CU是∠ACK的角平分线,
∴∠OCK=∠FCO,
∴∠FCO=∠FOC,
∴FO=CF,
∴BE=EO=FO+EF=EF+CF,
∴EF=BE-CF
-
科目: 来源: 题型:
查看答案和解析>>【题目】一位运动员推铅球,铅球运行时离地面的高度
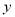 (米)是关于运行时间
(米)是关于运行时间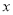 (秒)的二次函数.已知铅球刚出手时离地面的高度为
(秒)的二次函数.已知铅球刚出手时离地面的高度为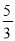 米;铅球出手后,经过4秒到达离地面3米的高度,经过10秒落到地面.如图建立平面直角坐标系.
米;铅球出手后,经过4秒到达离地面3米的高度,经过10秒落到地面.如图建立平面直角坐标系.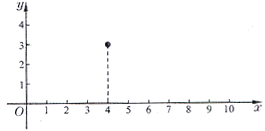
(Ⅰ)为了求这个二次函数的解析式,需要该二次函数图象上三个点的坐标.根据题意可知,该二次函数图象上三个点的坐标分别是____________________________;
(Ⅱ)求这个二次函数的解析式和自变量
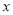 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(11·漳州)(满分8分)漳州市某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).请你根据图中所给的信息解答下列问题:
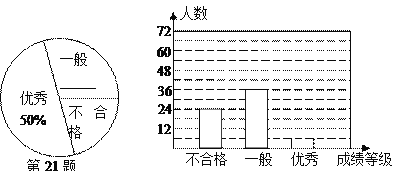
(1)请将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有_ ▲ 人达标;
(3)若该校学生有1200人,请你估计此次测试中,全校达标的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠ADC=90°,AD=8,CD=6,AB=26,BC=24.
(1)试说明:△ABC是直角三角形.
(2)请求图中阴影部分的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知正方形ABCD的边CD在正方形DEFG的边DE上,连接AE,GC.
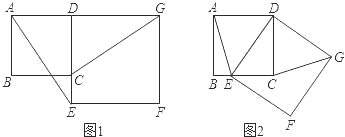
(1)试猜想AE与GC有怎样的位置关系,并证明你的结论;
(2)将正方形DEFG绕点D按顺时针方向旋转,使点E落在BC边上,如图2,连接AE和GC.你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.
-
科目: 来源: 题型:
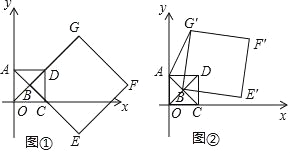
查看答案和解析>>【题目】在平面直角坐标系中,O为坐标原点,点A(0,1),点C(1,0),正方形AOCD的两条对角线的交点为B,延长BD至点G,使DG=BD,延长BC至点E,使CE=BC,以BG,BE为邻边作正方形BEFG.
(Ⅰ)如图①,求OD的长及
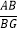 的值;
的值;(Ⅱ)如图②,正方形AOCD固定,将正方形BEFG绕点B逆时针旋转,得正方形BE′F′G′,记旋转角为α(0°<α<360°),连接AG′.
①在旋转过程中,当∠BAG′=90°时,求α的大小;
②在旋转过程中,求AF′的长取最大值时,点F′的坐标及此时α的大小(直接写出结果即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c.
(Ⅰ)若抛物线的顶点为A(﹣2,﹣4),抛物线经过点B(﹣4,0)
①求该抛物线的解析式;
②连接AB,把AB所在直线沿y轴向上平移,使它经过原点O,得到直线l,点P是直线l上一动点.
设以点A,B,O,P为顶点的四边形的面积为S,点P的横坐标为x,当4+6
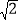 ≤S≤6+8
≤S≤6+8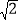 时,求x的取值范围;
时,求x的取值范围;(Ⅱ)若a>0,c>1,当x=c时,y=0,当0<x<c时,y>0,试比较ac与l的大小,并说明理由.
相关试题

