【题目】已知A、B、C三点不在同一直线上.
(1)若点A、B、C均在半径为R的⊙O上,
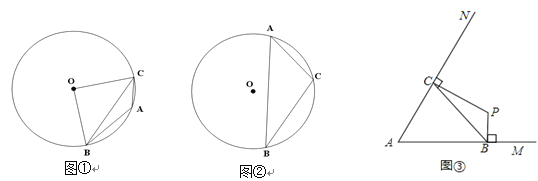
①如图①,当∠A=135°,R=1时,求∠BOC的度数和BC的长.
②如图②,当∠A为锐角时,求证: ![]() ;
;
(2)若定长线段BC的两个端点分别在∠MAN的两边AM、AN(B、C均与A不重合)滑动,如图③,当∠MAN=60°,BC=2时,分别作BP⊥AM,CP⊥AN,交点为P,试探索在整个滑动过程中,P、A两点间的距离是否保持不变?请说明理由.
参考答案:
【答案】(1)①∠BOC=90°,BC=![]() ,②证明见解析;(2)在整个滑动过程中,P、A两点间的距离是否保持不变,理由见解析.
,②证明见解析;(2)在整个滑动过程中,P、A两点间的距离是否保持不变,理由见解析.
【解析】试题分析:(1)①根据同弧所对的圆周角是圆心角的一半,因为∠A=135°,所以优弧所对的角∠BOC=270°,所以劣弧BC所对的∠BOC=90°,再由勾股定理计算出BC的长度;②延长CO交![]() O于点E,连接BE,所以∠A=∠E,因为CE为
O于点E,连接BE,所以∠A=∠E,因为CE为![]() 0的直径,得出∠CBE=90°,所以sinA=sinE=
0的直径,得出∠CBE=90°,所以sinA=sinE=![]() =
=![]() ;(2)连接AP,取AP的中点K,分别连接CK、BK,由于BP⊥AM,CP⊥AN,作KH⊥BC交BC于点H,根据直角三角形我们斜边上的中线等于斜边的一半,得CK=BK=AK=PK,即点A、B、P、C在以K为圆心,
;(2)连接AP,取AP的中点K,分别连接CK、BK,由于BP⊥AM,CP⊥AN,作KH⊥BC交BC于点H,根据直角三角形我们斜边上的中线等于斜边的一半,得CK=BK=AK=PK,即点A、B、P、C在以K为圆心, ![]() AP为半径的圆上,当定长线段BC的两个端点分别在∠MAN的两边AM、AN(B、C均与A不重合)滑动,如图,当∠MAN=60时,∠BKC=120,BC=2,即△BKC是一个顶角为120°,底边BC=2的等腰三角形,不难求出CK=BK=
AP为半径的圆上,当定长线段BC的两个端点分别在∠MAN的两边AM、AN(B、C均与A不重合)滑动,如图,当∠MAN=60时,∠BKC=120,BC=2,即△BKC是一个顶角为120°,底边BC=2的等腰三角形,不难求出CK=BK=![]() AP=
AP=![]() ,即AP=
,即AP=![]() ,所以在整个滑动过程中,P、A两点间的距离保持不变.
,所以在整个滑动过程中,P、A两点间的距离保持不变.
试题解析:
解(1)①根据同弧所对的圆周角是圆心角的一半,∵∠A=135°,
∴优弧所对的角∠BOC=270°,
∴劣弧BC所对的∠BOC=90°;
在Rt△BOC中,由勾股定理可知BC=![]() =
=![]() .
.
②
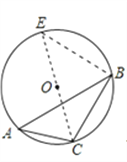
证明:如图所示,延长CO交![]() O于点E,连接BE,
O于点E,连接BE,
∴∠A=∠E,
∵CE为![]() 0的直径,
0的直径,
∴∠CBE=90°,
∴sinA=sinE=![]() =
=![]() .
.
(2)
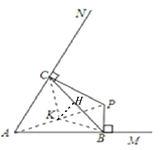
连接AP,取AP的中点K,分别连接CK、BK,作KH⊥BC交BC于点H,
∵BP⊥AM,CP⊥AN,K是AP的中点,
∴CK=BK=AK=PK,
∴点A、B、P、C在以K为圆心, ![]() AP为半径的圆上,
AP为半径的圆上,
∵∠MAN=60,
∴∠BKC=120,
∴∠KBC=30°,
∵BC=2,
∴BH=CH=![]() ,
,
∵cos30°=![]() =
=![]() ,
,
∴BK=![]() ,
,
∴CK=BK=![]() AP=
AP=![]() ,即AP=
,即AP=![]() .
.
所以在整个滑动过程中,P、A两点间的距离保持不变.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△AOB的三个顶点的坐标分别是A(-4,3),B(-6,0), O是原点.点M是OB边上异于O,B的一动点,过点M作MN//AB,点P是AB边上的任意点,连接AM,PM,PN,BN.设点
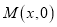 .
.(1)求出OA所在直线的解析式,并求出点M的坐标为(-1,0)时,点N的坐标.
(2)若
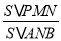 =
=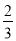 时,求此时点N的坐标.
时,求此时点N的坐标.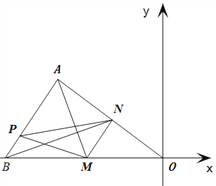
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,“和谐号”高铁列车的小桌板收起时,小桌板的支架底端与桌面顶端的距离OA=75厘米,且可以近似看作与地面垂直.展开小桌板使桌面保持水平,此时CB⊥AO,∠AOB=∠ACB=37°,且支架长OB与桌面宽BC的长度之和等于OA的长度.求小桌板桌面的宽度BC.(参考数据
 ,
, 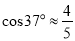 ,
, 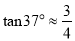 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,
, ,
,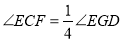 ,记
,记 ,则
,则 ________.
________.
-
科目: 来源: 题型:
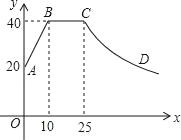
查看答案和解析>>【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB,BC分别为线段,CD为双曲线的一部分):
(1)分别求出线段AB和曲线CD的函数关系式;
(2)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(3)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将正方形 ABCD 绕点 A 按逆时针方向旋转到正方形AB ' C ' D ' ,旋转角为 ( 0<< 180 ) ,连接 B ' D 、 C ' D ,若 B ' D C ' D ,则 =____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
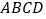 中,点
中,点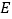 是
是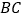 边上的一动点,点
边上的一动点,点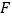 是
是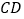 上一点,且
上一点,且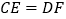 ,
,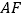 、
、 相交于点
相交于点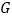 .
.(1)求证:
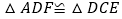 ;
;(2)求
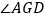 的度数
的度数(3)若
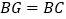 ,求
,求 的值.
的值.
相关试题

