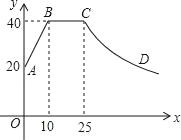
【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB,BC分别为线段,CD为双曲线的一部分):
(1)分别求出线段AB和曲线CD的函数关系式;
(2)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(3)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
参考答案:
【答案】(1)y1=2x+20.y2=![]() ;(2)第30分钟注意力更集中.(3)经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.
;(2)第30分钟注意力更集中.(3)经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.
【解析】
(1)用待定系数法分别求出AB和CD的函数表达式即可;
(2)分别求第五分钟和第三十分钟的注意力指数,最后比较判断;
(3)分别求出注意力指数为36时的两个时间,再将两时间之差和19比较,大于19则能讲完,否则不能.
解:(1)设线段AB所在的直线的解析式为y1=k1x+20,
把B(10,40)代入得,k1=2,
∴y1=2x+20.
设C、D所在双曲线的解析式为y2=![]() ,
,
把C(25,40)代入得,k2=1000,
∴y2=![]() .
.
(2)当x1=5时,y1=2×5+20=30,
当x2=30时,y2=![]() =
=![]() ,
,
∴y1<y2
∴第30分钟注意力更集中.
(3)令y1=36,
∴36=2x+20,
∴x1=8
令y2=36,
∴36=![]() ,
,
∴x2=![]() ≈27.8
≈27.8
∵27.8﹣8=19.8>19,
∴经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,“和谐号”高铁列车的小桌板收起时,小桌板的支架底端与桌面顶端的距离OA=75厘米,且可以近似看作与地面垂直.展开小桌板使桌面保持水平,此时CB⊥AO,∠AOB=∠ACB=37°,且支架长OB与桌面宽BC的长度之和等于OA的长度.求小桌板桌面的宽度BC.(参考数据
 ,
, 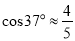 ,
, 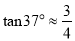 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,
, ,
,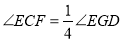 ,记
,记 ,则
,则 ________.
________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B、C三点不在同一直线上.
(1)若点A、B、C均在半径为R的⊙O上,
①如图①,当∠A=135°,R=1时,求∠BOC的度数和BC的长.
②如图②,当∠A为锐角时,求证:
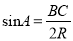 ;
;(2)若定长线段BC的两个端点分别在∠MAN的两边AM、AN(B、C均与A不重合)滑动,如图③,当∠MAN=60°,BC=2时,分别作BP⊥AM,CP⊥AN,交点为P,试探索在整个滑动过程中,P、A两点间的距离是否保持不变?请说明理由.
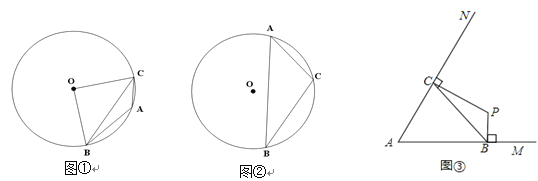
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将正方形 ABCD 绕点 A 按逆时针方向旋转到正方形AB ' C ' D ' ,旋转角为 ( 0<< 180 ) ,连接 B ' D 、 C ' D ,若 B ' D C ' D ,则 =____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
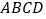 中,点
中,点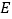 是
是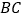 边上的一动点,点
边上的一动点,点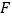 是
是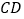 上一点,且
上一点,且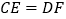 ,
,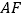 、
、 相交于点
相交于点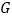 .
.(1)求证:
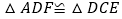 ;
;(2)求
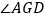 的度数
的度数(3)若
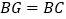 ,求
,求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:用2辆A型车和1辆B型车载满货物一次可运货11吨;用1辆A型车和2辆B型车载满货物一次可运货13吨.根据以上信息, 解答下列问题:
(1)1辆A型车和l辆B型车都载满货物一次可分别运货多少吨?
(2)某物流公司现有31吨货物,计划同时租用A型车
 辆,B型车
辆,B型车 辆,一次运完,且恰好每辆车都载满货物请用含有
辆,一次运完,且恰好每辆车都载满货物请用含有 的式子表示
的式子表示 ,并帮该物流公司设计租车方案;
,并帮该物流公司设计租车方案;(3)在(2)的条件下,若A型车每辆需租金500元/次,B型车每辆需租金600元/次.请选出最省钱的租车方案,并求出最少租车费用.
相关试题

