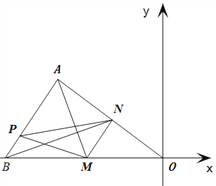
【题目】如图,在平面直角坐标系中,△AOB的三个顶点的坐标分别是A(-4,3),B(-6,0), O是原点.点M是OB边上异于O,B的一动点,过点M作MN//AB,点P是AB边上的任意点,连接AM,PM,PN,BN.设点![]() .
.
(1)求出OA所在直线的解析式,并求出点M的坐标为(-1,0)时,点N的坐标.
(2)若 ![]() =
=![]() 时,求此时点N的坐标.
时,求此时点N的坐标.
参考答案:
【答案】(1)![]() ;N(
;N(![]() ,
, ![]() );(2)N(
);(2)N(![]() ,2)
,2)
【解析】试题分析:(1)设y=kx(k≠0),将点A的坐标代入解析式求出k的值,写出解析式;(2)因为MN//AB,所以N点的横坐标与A点的横坐标之比为![]() ,又因为A的坐标已知,故可求出N点的横坐标,将N点的横坐标代入直线OA的解析式,即可求出N的纵坐标;(3)因为MN//AB,根据平行线间的距离相等,所以S△PMN=S△BMN,S△ANB=S△ABM,所以将
,又因为A的坐标已知,故可求出N点的横坐标,将N点的横坐标代入直线OA的解析式,即可求出N的纵坐标;(3)因为MN//AB,根据平行线间的距离相等,所以S△PMN=S△BMN,S△ANB=S△ABM,所以将![]() 转化为
转化为![]() ,已知hA,不难求出hN,将点N的坐标代入直线OA解析式即可求出N纵坐标.
,已知hA,不难求出hN,将点N的坐标代入直线OA解析式即可求出N纵坐标.
试题解析:
解:(1)由于A(-4,3),设直线OA为y=kx(k≠0),得y=-![]() x;
x;
又因OA=5,OB=6,OM=1,且MN//AB,
所以N点的横坐标与A点的横坐标之比为![]() ,
,
即点N的横坐标为-![]() ,代入y=-
,代入y=-![]() x得,N(-
x得,N(-![]() ,
, ![]() );
);
(2)∵MN//AB,根据平行线间的距离相等,
∴S△PMN=S△BMN,S△ANB=S△ABM,
∴![]() =
=![]() =
=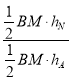 =
=![]() (其中
(其中![]() 、
、![]() 为A、N点的纵坐标),
为A、N点的纵坐标),
∴![]() ,
,
又∵A(-4,3),
∴hN=2,即yN=2,
将yN=2代入y=-![]() x,得x=-
x,得x=-![]() ,
,
∴N(-![]() ,2).
,2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=40°,点C在OA上,点P为OB上一动点,∠CPB的角平分线PD交射线OA于D。设∠OCP的度数为x°,∠CDP的度数为y°。

小明对x与y之间满足的等量关系进行了探究,
下面是小明的探究过程,请补充完整;
(1)x的取值范围是 ;
(2)按照下表中x的值进行取点、画图、计算,分别得到了y与x的几组对应值,补全表格;

(3)在平面直角坐标系xOy中,
①描出表中各组数值所对应的点(x,y);
②描出当x=120°时,y的值;
(4)若∠AOB=
 °,题目中的其它条件不变,用含
°,题目中的其它条件不变,用含 、x的代数式表示y为 。
、x的代数式表示y为 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 的顶点
的顶点 、
、 分别在
分别在 、
、 轴的正半轴上,点
轴的正半轴上,点 在反比例函数
在反比例函数 的第一象限内的图像上,
的第一象限内的图像上, ,
, ,动点
,动点 在
在 轴的上方,且满足
轴的上方,且满足 .
.(1)若点
 在这个反比例函数的图像上,求点
在这个反比例函数的图像上,求点 的坐标;
的坐标;(2)连接
 、
、 ,求
,求 的最小值;
的最小值;(3)若点
 是平面内一点,使得以
是平面内一点,使得以 、
、 、
、 、
、 为顶点的四边形是菱形,则请你直接写出满足条件的所有点
为顶点的四边形是菱形,则请你直接写出满足条件的所有点 的坐标.
的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列各组条件中,不能说明
 的是( )
的是( )A.AB=DE,∠B=∠E,∠C=∠FB.AB=DE,∠A=∠D,∠B=∠E
C.AC=DF,BC=EF,∠A=∠DD.AB=DE,BC=EF,AC=ED
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,“和谐号”高铁列车的小桌板收起时,小桌板的支架底端与桌面顶端的距离OA=75厘米,且可以近似看作与地面垂直.展开小桌板使桌面保持水平,此时CB⊥AO,∠AOB=∠ACB=37°,且支架长OB与桌面宽BC的长度之和等于OA的长度.求小桌板桌面的宽度BC.(参考数据
 ,
, 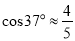 ,
, 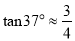 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,
, ,
,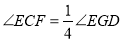 ,记
,记 ,则
,则 ________.
________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B、C三点不在同一直线上.
(1)若点A、B、C均在半径为R的⊙O上,
①如图①,当∠A=135°,R=1时,求∠BOC的度数和BC的长.
②如图②,当∠A为锐角时,求证:
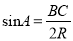 ;
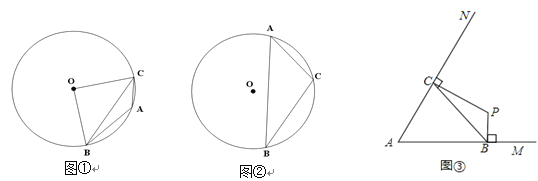
;(2)若定长线段BC的两个端点分别在∠MAN的两边AM、AN(B、C均与A不重合)滑动,如图③,当∠MAN=60°,BC=2时,分别作BP⊥AM,CP⊥AN,交点为P,试探索在整个滑动过程中,P、A两点间的距离是否保持不变?请说明理由.
相关试题

