【题目】在平面直角坐标系xOy中,已知一次函数y=kx+b(k≠0)的图象过点P(1,1),与x轴交于点A,与y轴交于点B,且tan∠ABO=3,那么点A的坐标是 .
参考答案:
【答案】(﹣2,0)或(4,0)
【解析】解:在Rt△AOB中,由tan∠ABO=3,可得OA=3OB,则一次函数y=kx+b中k=± ![]() . ∵一次函数y=kx+b(k≠0)的图象过点P(1,1),
. ∵一次函数y=kx+b(k≠0)的图象过点P(1,1),
∴当k= ![]() 时,求可得b=
时,求可得b= ![]() ;
;
k=﹣ ![]() 时,求可得b=
时,求可得b= ![]() .
.
即一次函数的解析式为y= ![]() x+
x+ ![]() 或y=﹣
或y=﹣ ![]() x+
x+ ![]() .
.
令y=0,则x=﹣2或4,
∴点A的坐标是(﹣2,0)或(4,0).
所以答案是:(﹣2,0)或(4,0).
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法,以及对锐角三角函数的定义的理解,了解锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:|﹣1|= , 2﹣2= , (﹣3)2= ,
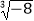 = .
= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B两个小集镇在河流CD的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?
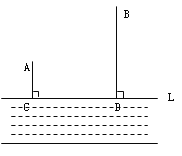
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,CE
 AD于点E,且CB=CE,点F为CD边上的一点,CB=CF,连接BF交CE于点G.
AD于点E,且CB=CE,点F为CD边上的一点,CB=CF,连接BF交CE于点G.(1)若
 ,CF=
,CF= ,求CG的长;
,求CG的长;(2)求证:AB=ED+CG

-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组和分式方程:
(1)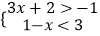 ;
;
(2)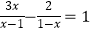 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接“六一”儿童节的到来,某校学生参加献爱心捐款活动,随机抽取该校部分学生的捐款数进行统计分析,相应数据的统计图如下:

(1)该样本的容量是 , 样本中捐款15元的学生有人;
(2)若该校一共有500名学生,据此样本估计该校学生的捐款总数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在四边形ABCD中,∠ABC+∠ADC=180°,AB=BC.
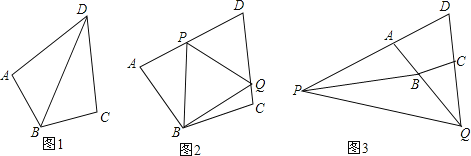
(1)如图1,若∠BAD=90°,AD=2,求CD的长度;
(2)如图2,点P、Q分别在线段AD、DC上,满足PQ=AP+CQ,求证:∠PBQ=90°
 ∠ADC;
∠ADC;(3)如图3,若点Q运动到DC的延长线上,点P也运动到DA的延长线上时,仍然满足PQ=AP+CQ,则(2)中的结论是否成立?若成立,请给出证明过程,若不成立,请写出∠PBQ与∠ADC的数量关系,并给出证明过程.
相关试题

