【题目】解不等式组和分式方程:
(1)![]() ;
;
(2)![]() .
.
参考答案:
【答案】
(1)解: ![]() ,
,
由①得:x>﹣1,
由②得:x>﹣2,
则不等式组的解集为:x>﹣1;
(2)解:去分母得:3x+2=x﹣1,
移项得:3x﹣x=﹣1﹣2,即2x=﹣3,
解得:x=﹣ ![]() ,
,
经检验x=﹣ ![]() 是分式方程的解.
是分式方程的解.
【解析】(1)分别求出不等式组中两不等式的解集,找出解集的公共部分即可;(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
【考点精析】本题主要考查了去分母法和一元一次不等式组的解法的相关知识点,需要掌握先约后乘公分母,整式方程转化出.特殊情况可换元,去掉分母是出路.求得解后要验根,原留增舍别含糊;解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )才能正确解答此题.
-
科目: 来源: 题型:
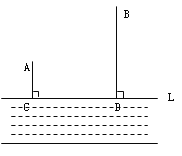
查看答案和解析>>【题目】如图,A、B两个小集镇在河流CD的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,CE
 AD于点E,且CB=CE,点F为CD边上的一点,CB=CF,连接BF交CE于点G.
AD于点E,且CB=CE,点F为CD边上的一点,CB=CF,连接BF交CE于点G.(1)若
 ,CF=
,CF= ,求CG的长;
,求CG的长;(2)求证:AB=ED+CG

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知一次函数y=kx+b(k≠0)的图象过点P(1,1),与x轴交于点A,与y轴交于点B,且tan∠ABO=3,那么点A的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接“六一”儿童节的到来,某校学生参加献爱心捐款活动,随机抽取该校部分学生的捐款数进行统计分析,相应数据的统计图如下:

(1)该样本的容量是 , 样本中捐款15元的学生有人;
(2)若该校一共有500名学生,据此样本估计该校学生的捐款总数. -
科目: 来源: 题型:
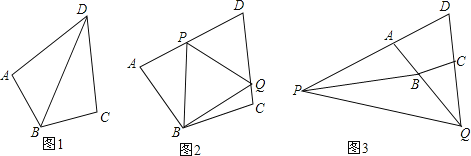
查看答案和解析>>【题目】已知在四边形ABCD中,∠ABC+∠ADC=180°,AB=BC.
(1)如图1,若∠BAD=90°,AD=2,求CD的长度;
(2)如图2,点P、Q分别在线段AD、DC上,满足PQ=AP+CQ,求证:∠PBQ=90°
 ∠ADC;
∠ADC;(3)如图3,若点Q运动到DC的延长线上,点P也运动到DA的延长线上时,仍然满足PQ=AP+CQ,则(2)中的结论是否成立?若成立,请给出证明过程,若不成立,请写出∠PBQ与∠ADC的数量关系,并给出证明过程.
-
科目: 来源: 题型:
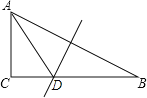
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,BC=15,斜边AB的垂直平分线与∠CAB的平分线都交BC于D点,则点D到斜边AB的距离为___________.
相关试题

