【题目】定义:只有一组对角是直角的四边形叫做损矩形,连结它的两个非直角顶点的线段叫做这个损矩形的直径.
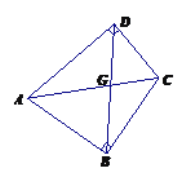
(1)如图,损矩形![]() 中,
中,![]() ,则该损矩形的直径是线段______.
,则该损矩形的直径是线段______.
(2)探究:在上述损矩形![]() 内,是否存在点
内,是否存在点![]() ,使
,使![]() 四个点都在以
四个点都在以![]() 为圆心的同一圆上,若存在,请指出点
为圆心的同一圆上,若存在,请指出点![]() 的具体位置___________________________;若不存在,请说明理由.
的具体位置___________________________;若不存在,请说明理由.
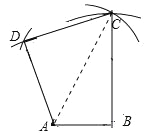
(3)实践:已知如图三条线段![]() ,求作相邻三边长顺次为
,求作相邻三边长顺次为![]() 的损矩形
的损矩形![]() (尺规作图,保留作图痕迹).
(尺规作图,保留作图痕迹).
参考答案:
【答案】(1)AC(2)O点为线段AC的中点(3)见解析
【解析】分析:(1)由损矩形的直径的定义即可得到答案;
(2)由![]() 可判定
可判定![]() 四点共圆,易得圆心是线段
四点共圆,易得圆心是线段![]() 的中点;
的中点;
(3)首先画线段![]() ,再以A为圆心,b长为半径画弧,再以B为圆心,c长为半径画弧,过点B作直线与以B为圆心的弧相交与点C,连接AC,以AC的中点为圆心,
,再以A为圆心,b长为半径画弧,再以B为圆心,c长为半径画弧,过点B作直线与以B为圆心的弧相交与点C,连接AC,以AC的中点为圆心,
![]() 为半径画弧,与以点A为圆心的弧交于点D,连接AD、DC,BC即可得到所求图形.
为半径画弧,与以点A为圆心的弧交于点D,连接AD、DC,BC即可得到所求图形.
详解:(1)由定义知,线段AC是该损矩形的直径,
故答案为:AC;
(2)∵![]()
∴![]()
∴A、B. C.D四点共圆,
∴在损矩形ABCD内存在点O,
使得A. B. C.D四个点都在以O为圆心的同一个圆上,
∵![]()
∴AC是⊙O的直径,
∴O是线段AC的中点;
(3)如图所示,四边形ABCD即为所求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在高处让一物体由静止开始落下,它下落的路程s与时间t之间的关系如下表:
时间t(秒)
1
2
3
4
5
落下路程s(米)
4.9×1
4.9×4
4.9×9
4.9×16
4.9×25
(1)请根据表格中的数据写出时间t与物体落下的路程s之间的关系;
(2)算出当t=4.5秒时,物体落下的路程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线y=ax2+bx﹣2与x轴交于点A(﹣1,0),B(4,0)两点,与y轴交于点C,经过点B的直线交y轴于点E(0,2).
(1)求该抛物线的解析式;
(2)如图2,过点A作BE的平行线交抛物线于另一点D,点P是抛物线上位于线段AD下方的一个动点,连结PA,EA,ED,PD,求四边形EAPD面积的最大值;
(3)如图3,连结AC,将△AOC绕点O逆时针方向旋转,记旋转中的三角形为△A′OC′,在旋转过程中,直线OC′与直线BE交于点Q,若△BOQ为等腰三角形,请直接写出点Q的坐标.

-
科目: 来源: 题型:
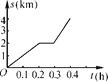
查看答案和解析>>【题目】小明骑自行车去学校,最初以某一速度匀速行驶,中途自行车发生故障,停下来修车耽误了几分钟,为了按时到校,他加快了速度,仍保持匀速行驶,结果准时到校,到校后,小明画了自行车行进路程s(km)与行进时间t(h)的图象,如图所示,请回答:
(1)这个图象反映了哪两个变量之间的关系?
(2)根据图象填表:
时间t/h
0
0.2
0.3
0.4
路程s/km
(3)路程s可以看成时间t的函数吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】良好行为习惯的养成,是中学生成长重要内容之一.某中学为了了解学生良好行为习惯养成的情况,该校七年级数学兴趣小组在校内随机抽取了部分同学进行调查评分,然后按各人得分高低分成“优秀”、“良好”、“一般”、“较差”四个等级,并绘制了如下两幅统计图(不完整):
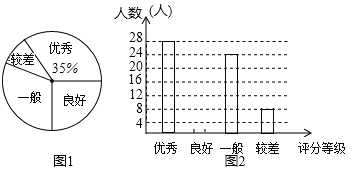
请你根据图中提供的信息,完成下列问题:
(1)图1中“优秀”部分所对应的圆心角为 .
(2)在如图2中,将“良好”部分的条形图补充完整;
(3)这次调查,良好行为习惯的养成“较差”人数占被调查人数的百分率为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】垃圾对环境的影响日益严重,垃圾危机的警钟被再次拉响.我市某中学积极响应国家号召,落实垃圾“分类回收,科学处理”的政策,准备购买
 、
、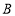 两种型号的垃圾分类回收箱共20只,放在校园各个合适位置,以方便师生进行垃圾分类投放.若购买
两种型号的垃圾分类回收箱共20只,放在校园各个合适位置,以方便师生进行垃圾分类投放.若购买 型14只、
型14只、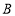 型6只,共需4240元;若购买
型6只,共需4240元;若购买 型8只、
型8只、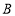 型12只,共需4480元.求
型12只,共需4480元.求 型、
型、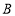 型垃圾分类回收箱的单价.
型垃圾分类回收箱的单价. -
科目: 来源: 题型:
查看答案和解析>>【题目】小王同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
月均用水量(单位:t)
频数
百分比
2≤x<3
2
4%
3≤x<4
12
24%
4≤x<5
5≤x<6
10
20%
6≤x<7
12%
7≤x<8
3
6%
8≤x<9
2
4%
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你估计总体小王所居住的小区中等用水量家庭大约有多少户?
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,请用列举法(画树状图或列表)求抽取出的2个家庭来自不同范围的概率.

相关试题

