【题目】阅读下列材料:
在学习“分式方程及其解法”过程中,老师提出一个问题:若关于x的分式方程![]() 的解为正数,求a的取值范围?
的解为正数,求a的取值范围?
经过小组交流讨论后,同学们逐渐形成了两种意见:
小明说:解这个关于x的分式方程,得到方程的解为x=a﹣2.由题意可得a﹣2>0,所以a>2,问题解决.
小强说:你考虑的不全面.还必须保证a≠3才行.
老师说:小强所说完全正确.
请回答:小明考虑问题不全面,主要体现在哪里?请你简要说明: .
完成下列问题:
(1)已知关于x的方程![]() =1的解为负数,求m的取值范围;
=1的解为负数,求m的取值范围;
(2)若关于x的分式方程![]() =﹣1无解.直接写出n的取值范围.
=﹣1无解.直接写出n的取值范围.
参考答案:
【答案】(1):m<![]() 且m≠﹣
且m≠﹣![]() ;(2)n=1或n=
;(2)n=1或n=![]() .
.
【解析】
考虑分式的分母不为0,即分式必须有意义;
(1)表示出分式方程的解,由解为负数确定出m的范围即可;
(2)分式方程去分母转化为整式方程,根据分式方程无解,得到有增根或整式方程无解,确定出n的范围即可.
请回答:小明没有考虑分式的分母不为0(或分式必须有意义)这个条件;
(1)解关于x的分式方程得,x=![]() ,
,
∵方程有解,且解为负数,
∴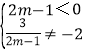 ,
,
解得:m<![]() 且m≠-
且m≠-![]() ;
;
(2)分式方程去分母得:3-2x+nx-2=-x+3,即(n-1)x=2,
由分式方程无解,得到x-3=0,即x=3,
代入整式方程得:n=![]() ;
;
当n-1=0时,整式方程无解,此时n=1,
综上,n=1或n=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知线段AB=12cm,点C为线段AB上的一动点,点D,E分别是AC和BC中点.
(1)若点C恰好是AB的中点,则DE=_______cm;
(2)若AC=4cm,求DE的长;
(3)试说明无论AC取何值(不超过12cm),DE的长不变;
(4)如图②,已知∠AOB=120°,过角的内部任一点C画射线OC.若OD,OE分别平分∠AOC和∠BOC.试说明∠DOE的度数与射线OC的位置无关.
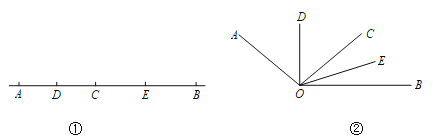
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,
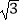 ),则点B的坐标为( )
),则点B的坐标为( ) 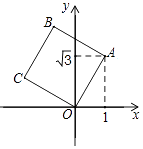
A.(1﹣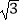 ,
, 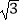 +1)
+1)
B.(﹣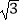 ,
, 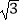 +1)??
+1)??
C.(﹣1,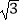 +1)
+1)
D.(﹣1,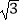 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)如图1,在四边形ABCD中,DC∥AB,AD=BC,BD平分∠ABC.

(1)求证:AD=DC;
(2)如图2,在上述条件下,若∠A=∠ABC=60°,过点D作DE⊥AB,过点C作CF⊥BD,垂足分别为E、F,连接EF.判断△DEF的形状并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )

A.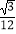
B.
C.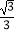
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
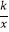 的图象经过二次函数y=ax2+bx图象的顶点(﹣
的图象经过二次函数y=ax2+bx图象的顶点(﹣  ,m)(m>0),则有( )
,m)(m>0),则有( ) 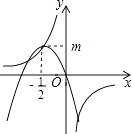
A.a=b+2k
B.a=b﹣2k
C.k<b<0
D.a<k<0 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(0,6),B(8,0),AB=10,如图作∠DBO=∠ABO,∠CAy=∠BAO,BD交y轴于点E,直线DO交AC于点C.
(1)①求证:△ACO≌△EDO;②求出线段AC、BD的位置关系和数量关系;
(2)动点P从A出发,沿A﹣O﹣B路线运动,速度为1,到B点处停止运动;动点Q从B出发,沿B﹣O﹣A运动,速度为2,到A点处停止运动.二者同时开始运动,都要到达相应的终点才能停止.在某时刻,作PE⊥CD于点E,QF⊥CD于点F.问两动点运动多长时间时△OPE与△OQF全等?

相关试题

