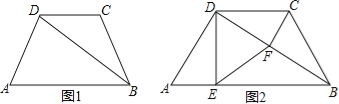
【题目】(题文)如图1,在四边形ABCD中,DC∥AB,AD=BC,BD平分∠ABC.

(1)求证:AD=DC;
(2)如图2,在上述条件下,若∠A=∠ABC=60°,过点D作DE⊥AB,过点C作CF⊥BD,垂足分别为E、F,连接EF.判断△DEF的形状并证明你的结论.
参考答案:
【答案】(1)证明见解析;(2)等边三角形,证明见解析
【解析】
试题(1)利用平行线的性质以及角平分线的性质得出对应角关系即可得出∠CDB=∠CBD进而得出AD=DC,
(2)利用等腰三角形的性质得出点F是BD的中点,再利用直角三角形的性质以及等边三角形的判定得出答案.
(1)证明:∵DC‖AB,
∴∠CDB=∠ABD,
又∵BD平分∠ABC,
∴∠CBD=∠ABD,
∴∠CDB=∠CBD,
∴BC=DC,
又∵AD=BC,
∴AD=DC;
(2)△DEF为等边三角形,
证明:∵BC=DC(已证),CF⊥BD,
∴点F是BD的中点,
∵∠DEB=90°,∴EF=DF=BF.
∵∠ABC=60°,BD平分∠ABC,∠BDE=60°,
∴△DEF为等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=30°,∠AOB内有一定点P,且OP=12,在OA上有一点Q,OB上有一点R,若△PQR周长最小,则最小周长是_____

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BD平分∠ABC,
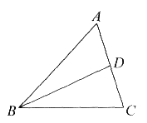
(1)作图:作BC边的垂直平分线分别交BC,BD于点E,F(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,连接CF,若∠A=60°,∠ABD=24°,求∠ACF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(π﹣3)0﹣(﹣1)2017+(﹣
 )﹣2+tan60°+|
)﹣2+tan60°+|  ﹣2|
﹣2| -
科目: 来源: 题型:
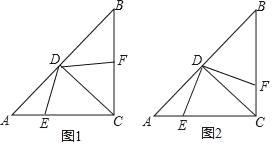
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,AC=BC,CD是∠ACB的角平分线,点E,F分别是边AC, BC上的动点,AC=4,设AE=x,BF=y.
(1)若x+y=3,求四边形CEDF的面积;
(2)当DE⊥DF时,如图2,试探索x、y之间的数量关系.
-
科目: 来源: 题型:
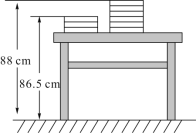
查看答案和解析>>【题目】新学期开学,两摞规格相同准备发放的数学课本整齐地叠放在讲台上,请根据图中所给的数据信息,解答下列问题:
(1)一本数学课本的高度是多少厘米?
(2)讲台的高度是多少厘米?
(3)请写出整齐叠放在桌面上的x本数学课本距离地面的高度的代数式(用含有x的代数式表示);
(4)若桌面上有56本同样的数学课本,整齐叠放成一摞,从中取走18本后,求余下的数学课本距离地面的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店在甲批发市场以每包m元的价格进了40包茶叶,又在乙批发市场以每包n元(m>n)的价格进了同样的60包茶叶,如果商家以每包
 元的价格卖出这种茶叶,卖完后,这家商店( )
元的价格卖出这种茶叶,卖完后,这家商店( )A.盈利了 B.亏损了 C.不赢不亏 D.盈亏不能确定
相关试题

