【题目】在Rt△ABC中,∠ACB=90°,AC=BC=2,点P为BC边上的一个动点(不与点B,C重合).点P关于直线AC,AB的对称点分别为M,N,连接MN交AC于点E,交AB于点F.
(1)当点P为线段BC的中点时,求∠M的正切值.
(2)当点P在线段BC上运动时(不与B,C重合),连接AM,AN,求证:
①△AMN为等腰直角三角形;
②△AEF∽△BAM.

参考答案:
【答案】(1)![]() ;(2)①见解析;②见解析.
;(2)①见解析;②见解析.
【解析】
(1)连接NB,根据对称的性质可证明BP=BN,进而证明∠MBN=90°,根据P为中点可证明MC=CP=PB=NB=1,求出∠M的正切值即可;(2)①如图:连接AP,根据对称性质可知AP=AM=AN,∠1=∠2,∠3=∠4,由∠CAB=∠2+∠3=45°证明∠MAN=90即可;②由∠AEF=∠5+∠1=45°+∠1,∠BAM=∠EAF+∠1=45°+∠1,可知∠AEF=∠BAM,再根据∠B==∠EAF=45°,即可证明△AEF∽△BAM.
(1)连接NB.
∵在Rt△ABC中,∠ACB=90°,AC=BC,
∴△ACB为等腰直角三角形,
∴∠A=∠CBA=45°.
∵点P关于直线AB的对称点为N,关于直线AC的对称点为M,
∴AB垂直PN,BN=BP,
∴∠NBA=∠PBA=45°,
∴∠PBN=90°,
∵P为BC的中点,BC=2,∴MC=CP=PB=NB=1,
∴tan ∠M=![]() .
.
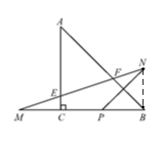
(2)①连接AP,如图.
∵点P关于直线AC,AB的对称点分别为M,N,
∴AP=AM=AN,∠1=∠2,∠3=∠4,
∵∠CAB=∠2+∠3=45°,
∴∠MAN=90°,
∴△AMN为等腰直角三角形.
②∵△AMN为等腰直角三角形,
∴∠5=∠6=45°,
∴∠AEF=∠5+∠1=45°+∠1,
∵∠EAF=45°,
∴∠BAM=∠EAF+∠1=45°+∠1,
∴∠AEF=∠BAM,
又∵∠B=∠BAC=45°,
∴△AEF∽△BAM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD和CD分别平分△ABC的内角∠EBA和外角∠ECA,BD交AC于F,连接AD.

(1)求证:∠BDC=
 ∠BAC;
∠BAC;(2)若AB=AC,请判断△ABD的形状,并证明你的结论;
(3)在(2)的条件下,若AF=BF,求∠EBA的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y1=
 的图象与一次函数y2=
的图象与一次函数y2= 的图象交于点A,B,点B的横坐标实数4,点P(1,m)在反比例函数y1=
的图象交于点A,B,点B的横坐标实数4,点P(1,m)在反比例函数y1= 的图象上.
的图象上.(1)求反比例函数的表达式;
(2)观察图象回答:当x为何范围时,y1>y2;
(3)求△PAB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在大课间活动中,同学们积极参加体育锻炼,小明就本班同学“我最喜爱的体育项目”进行了一次调查统计,下面是他通过收集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
(1)该班共有_____名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“乒乓球”部分所对应的圆心角度数为_____;
(4)学校将举办体育节,该班将推选5位同学参加乒乓球活动,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】满足下列条件的△ABC不是直角三角形的是()
A. BC=1,AC=2,AB=
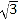
B. BC=1,AC=2,AB=
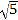
C. BC:AC:AB=3:4:5
D. ∠A:∠B:∠C=3:4:5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,工人师傅常用“卡钳”这种工具测定工件内槽的宽.卡钳由两根钢条AA′、BB′组成,O为AA′、BB′的中点.只要量出A′B′的长度,由三角形全等就可以知道工件内槽AB的长度.则判定△OAB≌△OA′B′的依据是( )

A. SASB. ASAC. SSSD. AAS
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一个池塘,其底面是边长为10尺的正方形,一个芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B′.则这根芦苇的长度是( )

A. 10尺 B. 11尺 C. 12尺 D. 13尺
相关试题

