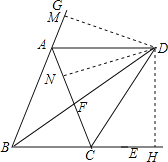
【题目】如图,BD和CD分别平分△ABC的内角∠EBA和外角∠ECA,BD交AC于F,连接AD.

(1)求证:∠BDC=![]() ∠BAC;
∠BAC;
(2)若AB=AC,请判断△ABD的形状,并证明你的结论;
(3)在(2)的条件下,若AF=BF,求∠EBA的大小.
参考答案:
【答案】(1)见解析;(2)△ABD为等腰三角形;见解析;(3)∠ABC=72°.
【解析】
试题分析:(1)根据角平分线的定义得到∠BDC+![]() ∠ABC=
∠ABC=![]() ∠ACE,∠BAC+∠ABC=∠ACE,于是得到∠BDC+
∠ACE,∠BAC+∠ABC=∠ACE,于是得到∠BDC+![]() ∠ABC=
∠ABC=![]() ∠BAC+
∠BAC+![]() ∠ABC,等量代换即可得到结论;
∠ABC,等量代换即可得到结论;
(2)作DM⊥BG于M,DN⊥AC于N,DH⊥BE于H根据角平分线的性质得到DM=DH,DN=DH,等量代换得到DM=DN,根据三角形的内角和得到∠GAD+∠CAD+∠BAC=180°,∠BAC+∠ABC+∠ACB=180°,推出∠GAD+∠CAD=∠ABC+∠ACB,由等腰三角形的性质得到∠ABC=∠ACB,等量代换得到∠GAD=∠ABC,推出AD∥BC,由平行线的性质得到∠ADB=∠DBC,证得∠ABD=∠ADB,即可得到结论;
(3)根据等腰三角形的性质得到∠BAF=∠ABF=![]() ∠ABC,根据三角形的内角和即可得到结论.
∠ABC,根据三角形的内角和即可得到结论.
解:(1)∵BD、CD分别平分∠EBA、∠ECA,BD交AC于F,
∴∠BDC+![]() ∠ABC=
∠ABC=![]() ∠ACE,∠BAC+∠ABC=∠ACE,
∠ACE,∠BAC+∠ABC=∠ACE,
∴∠BDC+![]() ∠ABC=
∠ABC=![]() ∠BAC+
∠BAC+![]() ∠ABC,
∠ABC,
∴∠BDC=![]() ∠BAC.
∠BAC.
(2)△ABD为等腰三角形,证明如下:
作DM⊥BG于M,DN⊥AC于N,DH⊥BE于H
∵BD、CD分别平分∠EBA、∠ECA,
∴DM=DH,DN=DH,
∴DM=DN,
∴AD平分∠CAG,即∠GAD=∠CAD,
∵∠GAD+∠CAD+∠BAC=180°,∠BAC+∠ABC+∠ACB=180°,
∴∠GAD+∠CAD=∠ABC+∠ACB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠GAD=∠ABC,
∴AD∥BC,
∴∠ADB=∠DBC,
又∵∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD,
∴△ABD为等腰三角形;
(3)∵AF=BF,
∴∠BAF=∠ABF=![]() ∠ABC,
∠ABC,
∵∠BAF+∠ABC+∠ACB=180°,∠ABC=∠ACB,
∴![]() ∠ABC=180°,
∠ABC=180°,
∴∠ABC=72°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c的图象如图所示,则|a﹣b+c|+|2a+b|=( )

A.a+b
B.a﹣2b
C.a﹣b
D.3a -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BCAD=
 AE2;④S△ABC=4S△ADF . 其中正确的有( )
AE2;④S△ABC=4S△ADF . 其中正确的有( ) 
A.1个
B.2 个
C.3 个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=2x2﹣2
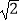 x+1与坐标轴的交点个数是 .
x+1与坐标轴的交点个数是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC 中,AB=AC=6cm,∠B=∠C,BC=4cm,点 D 为 AB的中点.
(1)如果点 P 在线段 BC 上以 1cm/s 的速度由点 B 向点 C 运动,同时,点 Q 在线段 CA 上由点 C 向点 A 运动.
①若点 Q 的运动速度与点 P 的运动速度相等,经过 1 秒后,△BPD 与△CQP 是否全等,请说明理由;
②若点 Q 的运动速度与点 P 的运动速度不相等,当点 Q 的运动速度为多少时,能够使△BPD 与△CQP 全等?
(2)若点 Q 以②中的运动速度从点 C 出发,点 P 以原来的运动速度从点 B 同时出发,都逆时针沿△ABC 三边运动,则经过 后,点 P 与点 Q 第一次在△ABC 的 边上相遇?(在横线上直接写出答案,不必书写解题过程)

-
科目: 来源: 题型:
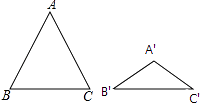
查看答案和解析>>【题目】如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠B+∠B′=90°,则△ABC与△A′B′C′的面积比为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两同学的家与学校的距离均为3000米.甲同学先步行600米,然后乘公交车去学校,乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的
 ,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家出发去学校,结果甲同学比乙同学早到2分钟.乙骑自行车的速度是( )米/分.
,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家出发去学校,结果甲同学比乙同学早到2分钟.乙骑自行车的速度是( )米/分.A. 600 B. 400 C. 300 D. 150
相关试题

