搜索
【题目】满足下列条件的△ABC不是直角三角形的是（）
A. BC＝1，AC＝2，AB＝
B. BC＝1，AC＝2，AB＝
C. BC：AC：AB＝3：4：5
D. ∠A：∠B：∠C＝3：4：5
参考答案：
【答案】D
【解析】
先求出两小边的平方和和最长边的平方，看看是否相等即可．
A．∵12+（
）2=22，∴△ABC是直角三角形，故本选项不符合题意；
B．∵12+22=（
）2，∴△ABC是直角三角形，故本选项不符合题意；
C．设BC=3x，则AC=4x，AB=5x．
∵（3x）2+（4x）2=（5x）2，∴△ABC是直角三角形，故本选项不符合题意；
D．∵∠A+∠B+∠C=180°，∠A：∠B：∠C=3：4：5，∴∠A=45°，∠5=60°，∠C=75°，∴△ABC不是直角三角形，故本选项符合题意．
故选D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知有一块等腰三角形纸板，在它的两腰上各有一点E和F，把这两点分别与底边中点连结，并沿着这两条线段剪下两个三角形，所得的这两个三角形相似，剩余部分（四边形）的四条边的长度如图所示，那么原等腰三角形的底边长为（ ）
A.
B. 
C. 
或
D. 
或
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，所有正方形的中心均在坐标原点，且各边与x轴或y轴平行，从内到外，它们的边长依此为2，4，6，8，...，顶点依此用A1，A2，A3，A4......表示，则顶点A55的坐标是___．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解
如图1，已知点A是BC外一点，连接AB，AC，求∠BAC+∠B+∠C的度数．
（1）阅读并补充下面推理过程
解：过点A作ED∥BC
∴∠B=∠ ，∠C=∠ ．
又∵∠EAB+∠BAC+∠DAC=180°（平角定义）
∴∠B+∠BAC+∠C=180°
从上面的推理过程中，我们发现平行线具有“等角转化”的功能，将∠BAC，∠B，∠C“凑”在一起，得出角之间的关系，使问题得以解决
（2）如图2，已知AB∥ED，求∠B+∠BCD+∠D的度数．
小明受到启发，过点C作CF∥AB如图所示，请你帮助小明完成解答：
（3）已知AB∥CD，点C在点D的右侧，∠ADC=70°．BE平分∠ABC，DE平分∠ADC，BE，DE所在的直线交于点E，点E在AB与CD两条平行线之间．
①如图3，点B在点A的左侧，若∠ABC=60°，则∠BED的度数为 °．
②如图4，点B在点A的右侧，且AB＜CD，AD＜BC．若∠ABC=n°，则∠BED的度数为 °（用含n的代数式表示）
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知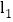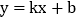直线
：
与直线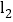
：
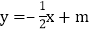都经过
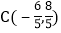，直线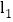交y轴于点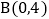
，交x轴于点A，直线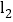交y轴于点D，P为y轴上任意一点，连接PA、PC，有以下说法：①方程组
的解为
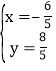；②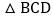
为直角三角形；③
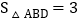；④当
的值最小时，点P的坐标为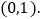
其中正确的说法个数有
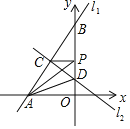
A. 1个B. 2个C. 3个D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了解同学对体育活动的喜爱情况，某校设计了“你最喜欢的体育活动是哪一项(仅限一项)”的调查问卷.该校对本校学生进行随机抽样调查，以下是根据调查数据得到的统计图的一部分.请根据以上信息解答以下问题：
(1)该校对多少名学生进行了抽样调查？
(2)请补全图1并标上数据.
(3)若该校共有学生900人，请你估计该校最喜欢跳绳项目的学生约有多少人？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某社区准备在甲、乙两位射箭爱好者中选出一人参加集训，两人各射了5剑，他们的总成绩
单位：环
相同，小宇根据他们的成绩绘制了尚不完整的统计图表，并计算了甲成绩的平均数和方差见小宇的作业．
______，
______；
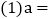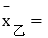请完成图中乙成绩变化情况的折线；
观察你补全的折线图可以看出______填“甲”或“乙”的成绩比较稳定
参照小宇的计算方法，计算乙成绩的方差，并验证你的判断；并判断谁将被选中．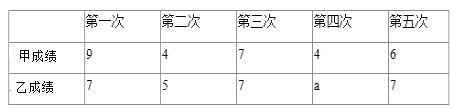
相关试题
