【题目】解不等式组与方程
(1)解不等式组 ![]()
(2)解方程: ![]() =
= ![]() ﹣3.
﹣3.
参考答案:
【答案】
(1)解: ![]() ,
,
解①得x<3,
解②得x≥ ![]() .
.
则不等式组的解集是: ![]() ≤x<3;
≤x<3;
(2)解:去分母,得﹣1=1﹣x﹣3(2﹣x),
去括号,得﹣1=1﹣x﹣6+3x,
移项,得﹣3x+x=1﹣6+1,
合并同类项,得﹣2x=﹣4,
系数化成1得x=2,
检验:当x=2时,2﹣x=0,则方程无解.
【解析】(1)首先解每个不等式,两个不等式解集的公共部分就是不等式组的解集;(2)去分母化成整式方程,解整式方程求得x的值,然后进行检验即可.
【考点精析】根据题目的已知条件,利用一元一次不等式组的解法的相关知识可以得到问题的答案,需要掌握解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图,△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=10,则△ADE周长是多少?为什么?
(2)若∠BAC=128°,则∠DAE的度数是多少?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)| ﹣2|+20140﹣(﹣
﹣2|+20140﹣(﹣  )﹣1+3tan30°
)﹣1+3tan30°
(2)先化简:1﹣ ÷
÷ 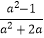 ,再选取一个合适的a值代入计算.
,再选取一个合适的a值代入计算. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某住宅小区在施工过程中留下了一块空地,已知AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABD和△AEC中,AD=AB,AE=AC,∠DAB=∠EAC=60°,CD、 BE相交于点P.
(1)用全等三角形判定方法证明:BE=DC
(2)求∠BPC的度数;
(3)在(2)的基础上,经过深入探究后发现:射线AP平分∠BPC,请判断你的发现是否正确,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E.

(1)求证:DE=AB.
(2)以D为圆心,DE为半径作圆弧交AD于点G.若BF=FC=1,试求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一个可以自由转动的转盘被平均分成3个扇形,分别标有1、2、3三个数字,小王和小李各转动一次转盘为一次游戏,当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转).

(1)请你用树状图或列表的方法表示出每次游戏可能出现的所有结果;
(2)两次转盘,第一次转得的数字记为m,第二次记为n,A的坐标为(m,n),则A点在函数y= 上的概率.
上的概率.
相关试题

