【题目】如图,在△ABC中,∠ACB=90°,CD平分∠ACB交AB于点D,将△CDB绕点C顺时针旋转到△CEF的位置,点F在AC上.
(1)△CDB旋转的度数;(2)连结DE,判断DE与BC的位置关系,并说明理由.
参考答案:
【答案】(1)△CDB旋转的度数:90°;(2)DE∥BC,见解析.
【解析】
(1)根据旋转的性质确定旋转角的度数;
(2)先利用旋转的性质得∠DCE=∠BCF=90°,CD=CE,则可判断△CDE为等腰直角三角形,所以∠CDE=45°,再利用角平分线定义得到∠BCD=45°,则∠CDE=∠BCD,然后根据平行线的判定方法可判断DE∥BC.
解:(1)∵将△CDB绕点C顺时针旋转到△CEF的位置,点F在AC上,
∴旋转角为∠BCF,
即旋转角为90°;
(2)DE∥BC.
理由如下:∵将△CDB绕点C顺时针旋转到△CEF的位置,点F在AC上,
∴∠DCE=∠BCF=90°,CD=CE,
∴△CDE为等腰直角三角形,
∴∠CDE=45°,
∵CD平分∠ACB交AB于点D,
∴∠BCD=45°,
∴∠CDE=∠BCD,
∴DE∥BC.
-
科目: 来源: 题型:
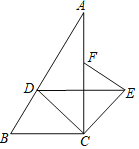
查看答案和解析>>【题目】如图,在
 中,
中, ,CD是高,BE平分∠ABC交CD于点E,EF∥AC交AB于点F,交BC于点G.在结论:(1)
,CD是高,BE平分∠ABC交CD于点E,EF∥AC交AB于点F,交BC于点G.在结论:(1) 
 ;(2)
;(2) 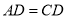 ;(3)
;(3)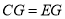 ;(4)
;(4) 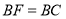 中,一定成立的有( )
中,一定成立的有( )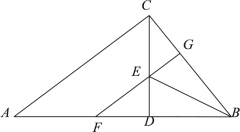
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将等腰
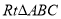 绕底角顶点A逆时针旋转15°后得到
绕底角顶点A逆时针旋转15°后得到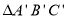 ,如果
,如果 ,那么两个三角形的重叠部分面积为____.
,那么两个三角形的重叠部分面积为____.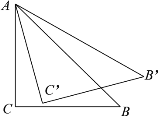
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备购买A、B两种奖品,奖励成绩优异的同学.已知购买1件A奖品和1件B奖品共需18元;购买30件A奖品和20件B奖品共需480元.
(1)A、B两种奖品的单价分别是多少元?
(2)如果学校购买两种奖品共100件,总费用不超过850元,那么最多可以购买A奖品多少件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高
 米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心
米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心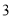 米.
米.
(1)请你建立适当的直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按
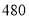 元销售时,每天可销售
元销售时,每天可销售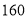 个;若销售单价每降低元,每天可多售出
个;若销售单价每降低元,每天可多售出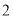 个.已知每个玩具的固定成本为
个.已知每个玩具的固定成本为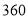 元,问这种玩具的销售单价为多少元时,厂家每天可获利润
元,问这种玩具的销售单价为多少元时,厂家每天可获利润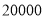 元?
元? -
科目: 来源: 题型:
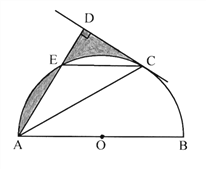
查看答案和解析>>【题目】如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD
 CD,垂足为D,AD交⊙O 于E,连接CE.(1)求证:CD 是⊙O 的切线
CD,垂足为D,AD交⊙O 于E,连接CE.(1)求证:CD 是⊙O 的切线(2)若E是弧AC的中点,⊙O 的半径为1,求图中阴影部分的面积。
相关试题

