【题目】如图所示,AE⊥AB,且AE=AB,BC⊥CD且BC=CD,若点E、B、D到直线AC的距离分别为6,3,4,则图中实现所围成的图像面积是( )

A. 50 B. 44 C. 38 D. 32
参考答案:
【答案】A
【解析】
由全等三角形的判定定理可得出△EFA≌△AGB,同理可证△BGC≌△CHD,从而得出FA、AG、GC、CH的长度,用割补法求出实线所围成的图像面积.
∵EA⊥AB,∴∠EAF+∠BAG=90°,
∵EF⊥AF,BG⊥AG,∴∠FEA+∠EAF=90°,∠EFA=∠BGA=90°,
∴∠BAG=∠FEA,
∵在△EFA与△AGB中,
 ,
,
∴△EFA≌△AGB,
∴BG=AF=3,EF=AG=6,
同理可证:△BGC≌△CHD,
∴GC=4,CH=3,
∴S=S梯形EFHD﹣2S△AEF﹣2S△CHD=![]() (4+6)×(3+6+3+4)﹣
(4+6)×(3+6+3+4)﹣![]() ×6×3×2﹣
×6×3×2﹣![]() ×4×3×2=50.
×4×3×2=50.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将函数y=x2的图象向右平移2个单位得函数y1的图象,将y与y1合起来构成新图象,直线y=m被新图象依次截得三段的长相等,则 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
 ,且
,且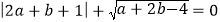 .
.(1)求
 的值;
的值;(2)①在
 轴的正半轴上存在一点
轴的正半轴上存在一点 ,使
,使 ,求点
,求点 的坐标;
的坐标;②在坐标轴上一共存在多少个点
 ,使
,使 成立?请直接写出符合条件的点
成立?请直接写出符合条件的点 的坐标.
的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,对于任意三点
中,对于任意三点 的“矩面积”,给出如下定义:“水平底”
的“矩面积”,给出如下定义:“水平底” 为任意两点横坐标差的最大值,“铅垂高”
为任意两点横坐标差的最大值,“铅垂高”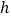 为任意两点纵坐标差的最大值,则“矩面积”
为任意两点纵坐标差的最大值,则“矩面积” .
.例如:三点坐标分别为
 ,则“水平底”
,则“水平底” ,“铅垂高”
,“铅垂高” ,“矩面积”
,“矩面积” .
.(1)已知点
 .
.①若
 三点的“矩面积”为12,求点
三点的“矩面积”为12,求点 的坐标;
的坐标;②求
 三点的“矩面积”的最小值.
三点的“矩面积”的最小值.(2)已知点
 ,其中
,其中 .若
.若 三点的“矩面积”为8,求
三点的“矩面积”为8,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,已知点P0的坐标为(
 ,
, ),将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn(n为正整数),则点P2017的坐标为( )
),将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn(n为正整数),则点P2017的坐标为( )
A. (
 ,
, ) B. (0,22018) C. (
) B. (0,22018) C. ( ,
, ) D. (22018,0)
) D. (22018,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠BAC=90°,AB=AC=2cm,线段BC上一动点P从C点开始运动,到B点停止,以AP为边在AC的右侧作等边△APQ,则Q点运动的路径为cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=﹣x2+bx+c的部分图象如图所示,A(1,0),B(0,3).
(1)求抛物线的解析式;
(2)结合函数图象,写出当y<3时x的取值范围.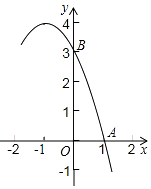
相关试题

