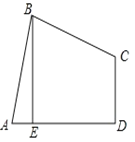
【题目】如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为16,则BE=( )
A.2B.3C.4D.5
参考答案:
【答案】C
【解析】
作BF⊥CD交CD的延长线于点F,根据直角三角形两锐角互余的关系可得∠ABE=∠CBF,利用AAS可证明△ABE≌△CBF,可得BE=BF;四边形ABCD的面积等于新正方形FBED的面积,根据∠BED=∠CDE=∠BFC=90°,可证明四边形BEDF是正方形,即可得BE=3.
过B作BF垂直DC的延长线于点F,
∵∠ABC=∠CDA=90°,BF⊥DF,
∴∠ABE+∠EBC=∠CBF+∠EBC,
∴∠ABE=∠CBF;
又∵BE⊥AD,BF⊥DF,且AB=BC,
∴△ABE≌△CBF,
∴BE=BF;四边形ABCD的面积等于四边形BEDF的面积
∵BE⊥AD,∠CDA=90°,DF⊥DF,
∴四边形BEDF是矩形,
又∵BE=BF,
∴四边形BEDF为正方形;
∵四边形ABCD的面积为16,
∴正方形BEDF的面积为16,
∴BE=4

故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图A在数轴上对应的数为-2.
(1)点B在点A右边距离A点4个单位长度,则点B所对应的数是_____.
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点B以每秒3个单位长度沿数轴向右运动.现两点同时运动,当点A运动到-6的点处时,求A、B两点间的距离.
(3)在(2)的条件下,现A点静止不动,B点以原速沿数轴向左运动,经过多长时间A、B两点相距4个单位长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系
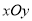 中,矩形
中,矩形 的边
的边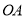 、
、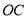 分别落在
分别落在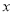 、
、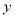 轴上,点
轴上,点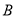 坐标为
坐标为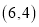 ,反比例函数
,反比例函数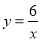 的图象与
的图象与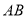 边交于点
边交于点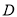 ,与
,与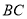 边交于点
边交于点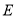 ,连结
,连结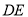 ,将
,将 沿
沿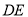 翻折至
翻折至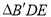 处,点
处,点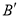 恰好落在正比例函数
恰好落在正比例函数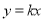 图象上,则
图象上,则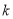 的值是
的值是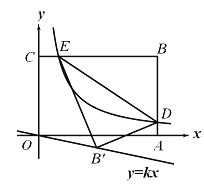
A.
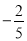 B.
B. 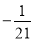 C.
C. 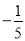 D.
D. 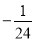
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
①8+(﹣10)+(﹣2)﹣(﹣5)
②2
 ﹣3
﹣3 ﹣5
﹣5 ﹣|﹣3
﹣|﹣3 |
|③(﹣1
 )+1.25+(﹣8.5)+10
)+1.25+(﹣8.5)+10
④(
 )×(﹣12)
)×(﹣12)⑤(﹣199
 )×5(用简便方法计算)
)×5(用简便方法计算)⑥10×(﹣
 )﹣2×
)﹣2× +(﹣3)×(﹣
+(﹣3)×(﹣ )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.(注:结果保留π )
(1)把圆片沿数轴向右滚动半周,点B到达数轴上点C的位置,点C表示的数是 数(填“无理”或“有理”),这个数是 ;
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是 ;
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣4,﹣3.
①第 次滚动后,A点距离原点最近,第 次滚动后,A点距离原点最远.
②当圆片结束运动时,A点运动的路程共有 ,此时点A所表示的数是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】庄子说:“一尺之椎,日取其半,万世不竭”.这句话(文字语言)表达了古人将事物无限分割的思想,用图形语言表示为图1,按此图分割的方法,可得到一个等式(符号语言):
 .图2也是一种无限分割:在
.图2也是一种无限分割:在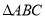 中,
中,  ,
,  ,过点
,过点 作
作 于点
于点 ,再过点
,再过点 作
作 于点
于点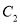 ,又过点
,又过点 作
作 于点
于点 ,如此无限继续下去,则可将
,如此无限继续下去,则可将 分割成
分割成 、
、 、
、 、
、 、…、
、…、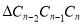 、….假设
、….假设 ,这些三角形的面积和可以得到一个等式是_________.
,这些三角形的面积和可以得到一个等式是_________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图(
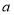 ),将两块直角三角尺的直角顶点
),将两块直角三角尺的直角顶点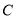 叠放在一起
叠放在一起
①若
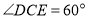 ,则
,则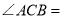 __________;若
__________;若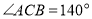 ,则
,则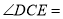 ___________.
___________.②猜想
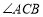 与
与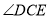 的度数有何特殊关系,并说明理由.
的度数有何特殊关系,并说明理由.(2)如图(
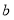 ),两个同样的三角尺
),两个同样的三角尺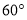 锐角的顶点
锐角的顶点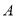 重合在一起,则
重合在一起,则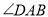 与
与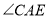 的度数有何关系?请说明理由.
的度数有何关系?请说明理由.(3)如图(
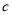 ),已知
),已知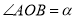 ,作
,作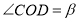 (
(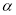 ,
,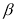 都是锐角且
都是锐角且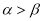 ),若
),若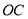 在
在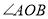 的内部,请直接写出
的内部,请直接写出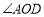 与
与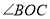 的度数关系.
的度数关系.
相关试题

