【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F. (Ⅰ)试判断直线BC与⊙O的位置关系,并说明理由;
(Ⅱ)若BD=2 ![]() ,BF=2,求阴影部分的面积(结果保留π).
,BF=2,求阴影部分的面积(结果保留π).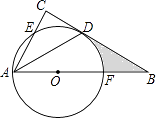
参考答案:
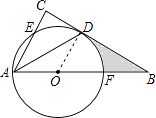
【答案】解:(Ⅰ)BC与⊙O相切. 证明:连接OD.
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD.
又∵OD=OA,
∴∠OAD=∠ODA.
∴∠CAD=∠ODA.
∴OD∥AC.
∴∠ODB=∠C=90°,即OD⊥BC.
又∵BC过半径OD的外端点D,
∴BC与⊙O相切.
(Ⅱ)设OF=OD=x,则OB=OF+BF=x+2,
根据勾股定理得:OB2=OD2+BD2 , 即(x+2)2=x2+12,
解得:x=2,即OD=OF=2,
∴OB=2+2=4,
∵Rt△ODB中,OD= ![]() OB,
OB,
∴∠B=30°,
∴∠DOB=60°,
∴S扇形AOB= ![]() =
= ![]() ,
,
则阴影部分的面积为S△ODB﹣S扇形DOF= ![]() ×2×2
×2×2 ![]() ﹣
﹣ ![]() =2
=2 ![]() ﹣
﹣ ![]() .
.
故阴影部分的面积为2 ![]() ﹣
﹣ ![]() .
.
【解析】(Ⅰ)连接OD,证明OD∥AC,即可证得∠ODB=90°,从而证得BC是圆的切线; (Ⅱ)在直角三角形OBD中,设OF=OD=x,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即为圆的半径,求出圆心角的度数,直角三角形ODB的面积减去扇形DOF面积即可确定出阴影部分面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)将△ABC向下平移3个单位长度,再向右平移2个单位长度,画出平移后的△A1B1C1;并写出顶点A1、B1、C1各点的坐标;
(2)计算△A1B1C1的面积。

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,因为直线AB、CD相交于点P,AB∥EF,所以CD不平行于EF(________________________________________________________);
(2)因为直线a∥b,b∥c,所以a∥c(________________________________).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下面的方格纸中,找出互相平行的线段,并用符号表示出来:__________,__________.
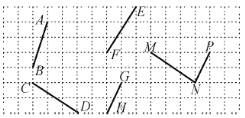
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点P在CA的延长线上,∠CAD=45°.
(Ⅰ)若AB=4,求 的长;
的长;
(Ⅱ)若 =
=  ,AD=AP,求证:PD是⊙O的切线.
,AD=AP,求证:PD是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地地震发生后,全国人民纷纷向灾区人民献出爱心。小华准备将平时节约的一些零用钱储存起来,然后捐给灾区的学生,她已存有62元,从现在起每个月存12元;小华的同学小丽也想捐钱给灾区的学生,小丽以前没有存过零用钱,听到小华在存零用钱,她表示从现在起每个月存20元,争取超过小华。
(1)试写出小华的存款总数y1与从现在开始的月数x之间的函数关系式以及小丽的存款数y2与月数x之间的函数关系式;
(2)从第几个月开始小丽的存款数可以超过小华?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AB﹦AC,BD、CE分别是所在角的平分线,AN⊥BD于N点,AM⊥CE于M点。求证:AM﹦AN
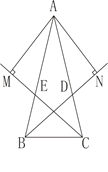
相关试题

