【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点P在CA的延长线上,∠CAD=45°.
(Ⅰ)若AB=4,求 ![]() 的长;
的长;
(Ⅱ)若 ![]() =
= ![]() ,AD=AP,求证:PD是⊙O的切线.
,AD=AP,求证:PD是⊙O的切线.
参考答案:
【答案】解:(Ⅰ)连接OC,OD, 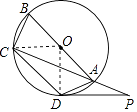
∵∠COD=2∠CAD,∠CAD=45°,
∴∠COD=90°,
∵AB=4,
∴OC= ![]() AB=2,
AB=2,
∴ ![]() 的长=
的长= ![]() ×π×2=π;
×π×2=π;
(Ⅱ)∵ ![]() =
= ![]() ,
,
∴∠BOC=∠AOD,
∵∠COD=90°,
∴∠AOD=45°,
∵OA=OD,
∴∠ODA=∠OAD,
∵∠AOD+∠ODA=∠OAD=180°,
∴∠ODA=67.5°,
∵AD=AP,
∴∠ADP=∠APD,
∵∠CAD=∠ADP+∠APD,∠CAD=45°,
∴∠ADP= ![]() CAD=22.5°,
CAD=22.5°,
∴∠ODP=∠ODA+∠ADP=90°,
∴PD是⊙O的切线.
【解析】(Ⅰ)连接OC,OD,由圆周角定理得到∠COD=2∠CAD,∠CAD=45°,于是得到∠COD=90°,根据弧长公式即可得到结论;(Ⅱ)由已知条件得到∠BOC=∠AOD,由圆周角定理得到∠AOD=45°,根据等腰三角形的性质得到∠ODA=∠OAD,求得∠ADP= ![]() CAD=22.5°,得到∠ODP=∠ODA+∠ADP=90°,于是得到结论.
CAD=22.5°,得到∠ODP=∠ODA+∠ADP=90°,于是得到结论.
【考点精析】根据题目的已知条件,利用圆内接四边形的性质和切线的判定定理的相关知识可以得到问题的答案,需要掌握把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,因为直线AB、CD相交于点P,AB∥EF,所以CD不平行于EF(________________________________________________________);
(2)因为直线a∥b,b∥c,所以a∥c(________________________________).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下面的方格纸中,找出互相平行的线段,并用符号表示出来:__________,__________.
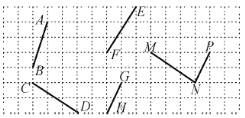
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F. (Ⅰ)试判断直线BC与⊙O的位置关系,并说明理由;
(Ⅱ)若BD=2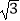 ,BF=2,求阴影部分的面积(结果保留π).
,BF=2,求阴影部分的面积(结果保留π).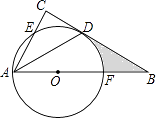
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地地震发生后,全国人民纷纷向灾区人民献出爱心。小华准备将平时节约的一些零用钱储存起来,然后捐给灾区的学生,她已存有62元,从现在起每个月存12元;小华的同学小丽也想捐钱给灾区的学生,小丽以前没有存过零用钱,听到小华在存零用钱,她表示从现在起每个月存20元,争取超过小华。
(1)试写出小华的存款总数y1与从现在开始的月数x之间的函数关系式以及小丽的存款数y2与月数x之间的函数关系式;
(2)从第几个月开始小丽的存款数可以超过小华?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AB﹦AC,BD、CE分别是所在角的平分线,AN⊥BD于N点,AM⊥CE于M点。求证:AM﹦AN
-
科目: 来源: 题型:
查看答案和解析>>【题目】作图题:(只保留作图痕迹)如图,在方格纸中,有两条线段AB、BC.利用方格纸完成以下操作:
(1)过点A作BC的平行线;
(2)过点C作AB的平行线,与(1)中的平行线交于点D;
(3)过点B作AB的垂线.
相关试题

