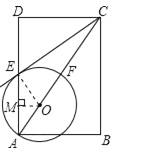
【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE.
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB=![]() ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径.

参考答案:
【答案】(1)直线CE与⊙O相切;(2)![]() .
.
【解析】
试题分析:(1)连接OE.欲证直线CE与⊙O相切,只需证明∠CEO=90°,即OE⊥CE即可;
(2)在直角三角形ABC中,根据三角函数的定义可以求得AB=![]() ,然后根据勾股定理求得AC=
,然后根据勾股定理求得AC=![]() ,同理知DE=1;
,同理知DE=1;
方法一、在Rt△COE中,利用勾股定理列出关于r的方程,从而易得r的值;
方法二、过点O作OM⊥AE于点M,在Rt△AMO中,根据三角函数的定义可以求得r的值.
试题解析:(1)直线CE与⊙O相切.理由如下:
∵四边形ABCD是矩形,∴BC∥AD,∠ACB=∠DAC;又∵∠ACB=∠DCE,∴∠DAC=∠DCE;连接OE,则∠DAC=∠AEO=∠DCE;∵∠DCE+∠DEC=90°,∴∠AE0+∠DEC=90°,∴∠OEC=90°,即OE⊥CE.
又OE是⊙O的半径,∴直线CE与⊙O相切.
(2)∵tan∠ACB=![]() =
=![]() ,BC=2,∴AB=BCtan∠ACB=
,BC=2,∴AB=BCtan∠ACB=![]() ,∴AC=
,∴AC=![]() ;又∵∠ACB=∠DCE,∴tan∠DCE=tan∠ACB=
;又∵∠ACB=∠DCE,∴tan∠DCE=tan∠ACB=![]() ,∴DE=DCtan∠DCE=1;
,∴DE=DCtan∠DCE=1;
方法一:在Rt△CDE中,CE=![]() =
=![]() ,连接OE,设⊙O的半径为r,则在Rt△COE中,
,连接OE,设⊙O的半径为r,则在Rt△COE中,![]() ,即
,即![]() ,解得:r=
,解得:r=![]() ;
;
方法二:AE=AD﹣DE=1,过点O作OM⊥AE于点M,则AM=![]() AE=
AE=![]() ,在Rt△AMO中,OA=
,在Rt△AMO中,OA=![]() =
=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用代数式表示“m的2倍与n平方的差”,正确的是( )
A.(2m-n)2 B.2(m-n)2 C.2m-n2 D.(m-2n)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】“若|a|>1,则a>1”是一个假命题,可以用举反例的方法说明它是假命题,下列选项中恰当的反例是( )
A.a=5B.a=﹣5C.a=1D.a=﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1) 4-3x=6-5x (2)5(x+8)﹣5=6(2x﹣7)
(3)
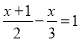 (4)
(4) 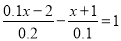
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校认真开展学习和实践科学发展观活动,在阶段总结中提出对本单位今后的整改措施,并在征求教职工对整改方案的满意程度时进行民主测评,测评等级为:很满意、较满意、满意、不满意四个等级.
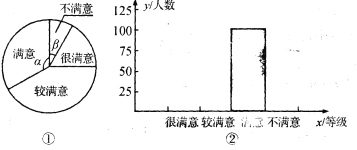
(1)若测评后结果如扇形图(图①),且测试等级为很满意、较满意、满意、不满意的人数之比为3:6:5:1,则图中a= 度,β= 度.
(2)若测试后部分统计结果如直方图(图②),请将直方图补画完整,并求出该单位职工总人数为 人.
(3)按上级要求,满意度必须不少于95%方案才能通过,否则,必须对方案进行完善.若要使该方案完善后能获得通过,至少还需增加 人对该方案的测评等级达满意(含满意)以上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若直线l1与直线y=3x﹣2关于x轴对称,则直线l1的关系式为( )
A.y=﹣3x﹣2B.y=﹣3x+2C.y=3x+2D.无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】二元一次方程2x+y=5的正整数解有( )
A.1个
B.2个
C.3个
D.4个
相关试题

