【题目】如图,已知OM平分∠AOC,ON平分∠BOC,∠AOB=90°,∠BOC=30°. 求: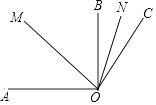
(1)∠AOC的度数;
(2)∠MON的度数.
参考答案:
【答案】
(1)解:∵∠AOC=∠AOB+∠BOC,
又∠AOB=90°,∠BOC=30°,
∴∠AOC=120°
(2)解:∵OM平分∠AOC,
∴∠MOC= ![]() ∠AOC,
∠AOC,
∵∠AOC=120°,
∴∠MOC=60°,
∵ON平分∠BOC,
∴∠NOC= ![]() ∠BOC,
∠BOC,
∵∠BOC=30°,
∴∠NOC=15°,
∵∠MON=∠MOC﹣∠NOC,
∴∠MON=45°
【解析】(1)根据角的和差即可得到结论;(2)根据角平分线的定义得到∠MOC= ![]() ∠AOC,∠NOC=
∠AOC,∠NOC= ![]() ∠BOC,于是得到结论.
∠BOC,于是得到结论.
【考点精析】掌握角的运算是解答本题的根本,需要知道角之间可以进行加减运算;一个角可以用其他角的和或差来表示.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线,交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简再求值:(ab+3a2)﹣2b2﹣5ab﹣2(a2﹣2ab),其中:a=1,b=﹣2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程
 +
+ 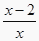 =
= 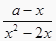 恰有一个实根,则满足条件的实数a的值的个数为( ).
恰有一个实根,则满足条件的实数a的值的个数为( ).
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法解下列方程:
(1)(x﹣2)(x﹣3)=12;
(2)3x2﹣6x+4=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C是线段AB上一点,点M、N、P分别是线段AC、BC、AB的中点,AC=3cm,CP=1cm,求:

(1)线段AM的长;
(2)线段PN的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC∽△A′B′C′,△ABC的三边之比为3:4:5.若△A′B′C′的最长边为20cm,则它的最短边长为cm.
相关试题

