【题目】已知关于x的方程 ![]() +
+ ![]() =
= ![]() 恰有一个实根,则满足条件的实数a的值的个数为( ).
恰有一个实根,则满足条件的实数a的值的个数为( ).
A.1
B.2
C.3
D.4
参考答案:
【答案】B
【解析】先将原方程变形,转化为整式方程后得2x2﹣3x+(4﹣a)=0①.由于原方程只有一个实数根,因此,方程①的根有两种情况:(1)方程①有两个相等的实数根,此二等根使x(x﹣2)≠0;(2)方程①有两个不等的实数根,而其中一根使x(x﹣2)=0,另外一根使x(x﹣2)≠0.针对每一种情况,分别求出a的值及对应的原方程的根.
去分母,将原方程两边同乘x(x﹣2),整理得2x2﹣3x+(4﹣a)=0.①
方程①的根的情况有两种:
第一,方程①有两个相等的实数根,即△=9﹣4×2(4﹣a)=0.
解得a= ![]() .
.
当a= ![]() 时,解方程2x2﹣3x+(﹣
时,解方程2x2﹣3x+(﹣ ![]() +4)=0,得x1=
+4)=0,得x1= ![]() ,x2=
,x2= ![]() .
.
第二,方程①有两个不等的实数根,而其中一根使原方程分母为零,即方程①有一个根为0或2.
(i)当x=0时,代入①式得4﹣a=0,即a=4.
当a=4时,解方程2x2﹣3x=0,x(2x﹣3)=0,x1=0或x2=1.5.
而x1=0是增根,即这时方程①的另一个根是x=1.5.它不使分母为零,确是原方程的唯一根.
(ii)当x=2时,代入①式,得2×4﹣2×3+(4﹣a)=0,即a=6.
当a=6时,解方程2x2﹣3x+2=0,该方程无解.
因此,若原分式方程只有一个实数根时,所求的a的值分别是 ![]() ,4,共2个.
,4,共2个.
故选:B.
【考点精析】利用分式方程的解对题目进行判断即可得到答案,需要熟知分式方程无解(转化成整式方程来解,产生了增根;转化的整式方程无解);解的正负情况:先化为整式方程,求整式方程的解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年我市有1.6万名初中毕业生参加升学考试,为了了解这1.6万名考生的数学成绩,从中抽取2000名考生的数学成绩进行统计,在这个问题中样本是( )
A. 1.6万名考生 B. 2000名考生 C. 1.6万名考生的数学成绩 D. 2000名考生的数学成绩
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线,交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简再求值:(ab+3a2)﹣2b2﹣5ab﹣2(a2﹣2ab),其中:a=1,b=﹣2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知OM平分∠AOC,ON平分∠BOC,∠AOB=90°,∠BOC=30°. 求:
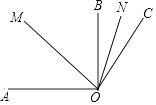
(1)∠AOC的度数;
(2)∠MON的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法解下列方程:
(1)(x﹣2)(x﹣3)=12;
(2)3x2﹣6x+4=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C是线段AB上一点,点M、N、P分别是线段AC、BC、AB的中点,AC=3cm,CP=1cm,求:

(1)线段AM的长;
(2)线段PN的长.
相关试题

