【题目】如图,等腰梯形ABCD中,AB∥CD,AB=2CD,AC交BD于点O,点E、F分别为AO、BO的中点,则下列关于点O成中心对称的一组三角形是( )
A.△ABO与△CDO
B.△AOD与△BOC
C.△CDO与△EFO
D.△ACD与△BCD
参考答案:
【答案】C
【解析】利用全等三角形的判定方法得到△CDO与△EFO全等,即其是关于点O成中心对称的一组三角形.
∵点E、F分别为AO、BO的中点,
∴AB=2EF,EF∥AB,
∵AB∥CD,
∴CD∥EF,
∴∠CDO=∠OFE,∠DCO=∠FEO,
∵AB=2CD,AB=2EF,
∴EF=CD,
∴△CDO≌△EFO,
即关于点O成中心对称的一组三角形是△CDO与△EFO.
故选C.
【考点精析】本题主要考查了等腰梯形的性质和中心对称及中心对称图形的相关知识点,需要掌握等腰梯形的两腰相等;同一底上的两个角相等;两条对角线相等;如果把一个图形绕着某一点旋转180度后能与另一个图形重合,那么我们就说,这两个图形成中心对称;如果把一个图形绕着某一点旋转180度后能与自身重合,那么我们就说,这个图形成中心对称图形才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题:
(1)11
 -1
-1 -1
-1 +4
+4 ;
;(2)(-22.84)-(+38.57)+(-37.16)-(-32.57);
(3)1
 -
- +2
+2 +
+ -4
-4 ;
;(4)(-36)-(-28)+(+125)+(-4)-(+53)-(-40).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E,F是四边形ABCD对角线AC上的两点,AD∥BC,DF∥BE,AE=CF.
求证:(1)△AFD≌△CEB;
(2)四边形ABCD是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在梯形ABCD中,AD∥BC,对角线AC和BD交于点O,下列条件中,能判断梯形ABCD是等腰梯形的是( )
A.∠BDC =∠BCD
B.∠ABC =∠DAB
C.∠ADB =∠DAC
D.∠AOB =∠BOC -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AD//BC,∠B=70°,∠C=40°,DE//AB交BC于点E.若AD=3cm,BC=10cm,则CD的长是 cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数.(如下表)
每人加工零件数
54
45
30
24
21
12
人 数
1
1
2
6
3
2
(1)写出这15人该月加工零件数的平均数、中位数和众数;
(2)假设生产部负责人把每位工人的月加工零件数定为24件,你认为是否合理?为什么?如果不合理,请你设计一个较为合理的生产定额,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为鼓励市民节约用电,小亮家所在地区规定:每户居民如果一个月的用电量不超过
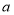 度,那么这户居民这个月只需交
度,那么这户居民这个月只需交 元电费;如果超过
元电费;如果超过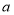 度,则这个月除了仍要交
度,则这个月除了仍要交 元的电费以外,超过的部分还要按每度
元的电费以外,超过的部分还要按每度 元交电费.已知小亮家
元交电费.已知小亮家 月份用电
月份用电 度,交电费
度,交电费 元;
元; 月份用电
月份用电 度,交电费
度,交电费 元.
元.(1)请直接写出小亮家
 月份超过
月份超过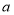 度部分的用电量(用含
度部分的用电量(用含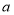 的代数式表示);
的代数式表示);(2)求
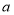 的值.
的值.
相关试题

