【题目】如图，E，F是四边形ABCD对角线AC上的两点，AD∥BC，DF∥BE，AE=CF．

求证：（1）△AFD≌△CEB；

（2）四边形ABCD是平行四边形．

参考答案：

【答案】（1）证明见解析；（2）证明见解析.

【解析】

（1）根据全等三角形的判定定理ASA证得△AFD≌△CEB；
（2）利用（1）中的全等三角形的对应边相等得到AD=CB，则由“有一组对边相等且平行的四边形是平行四边形”证得结论．

证明：（1）如图，

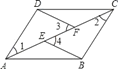
∵AD∥BC，DF∥BE，∴∠1=∠2，∠3=∠4．

又AE=CF，∴AE+EF=CF+EF，即AF=CE．

在△AFD与△CEB中，

，

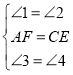∴△AFD≌△CEB（ASA）；

（2）由（1）知，△AFD≌△CEB，则AD=CB．

又∵AD∥BC，

∴四边形ABCD是平行四边形．

关闭