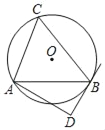
【题目】如图,⊙O的半径为5,△ABC是⊙O的内接三角形,AB=8.AD和过点B的切线互相垂直,垂足为D.
(1)求证:∠BAD+∠C=90°;
(2)求线段AD的长.
参考答案:
【答案】(1)证明见解析;(2)6.4
【解析】
(1)连接BO延长交⊙O于E,连接AE,根据切线的性质、结合题意得到AD∥BE,根据平行线的性质、圆周角定理证明;
(2)证明△ABE∽△DAB,根据相似三角形的性质得到比例式,计算即可.
(1)连接BO延长交⊙O于E,连接AE,
∵DB为⊙O的切线,
∴EB⊥BD,
∵AD⊥BD,
∴AD∥BE,
∴∠BAD=∠EBA,
∵BE为直径,
∴∠EBA+∠E=90°,
由圆周角定理得,∠E=∠C,
∴∠BAD+∠C=90°;

(2)∵⊙O的半径为5,
∴BE=10.
∵∠BAD=∠EBA,∠D=∠BAE,
∴△ABE∽△DAB,
∴![]() ,
,
∵AB=8,BE=10,
∴AD=6.4,
∴线段AD的长度为6.4.
-
科目: 来源: 题型:
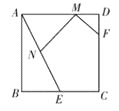
查看答案和解析>>【题目】如图,在正方形ABCD中,AB=4,E是BC边的中点, F是CD边上的一点, 且DF=1.若M、N分别是线段AD、AE上的动点,则MN+MF的最小值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:如图1,在△ABC中,当DE∥BC时可以得到三组成比例线段:①
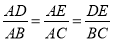 ;②
;② 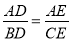 ;③
;③ 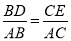 .反之,当对应线段程比例时也可以推出DE∥BC.
.反之,当对应线段程比例时也可以推出DE∥BC.理解运用:三角形的内接四边形是指顶点在三角形各边上的四边形.
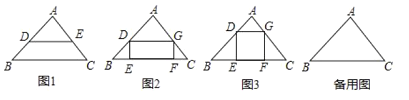
(1)如图2,已知矩形DEFG是△ABC的一个内接矩形,将矩形DEFG沿CB方向向左平移得矩形PBQH,其中顶点D、E、F、G的对应点分别为P、B、Q、H,在图2中画出平移后的图形;
(2)在(1)所得的图形中,连接CH并延长交BP的延长线于点R,连接AR.求证:AR∥BC;
(3)如图3,某小区有一块三角形空地,已知△ABC空地的边AB=400米,BC=600米,∠ABC=45°;准备在△ABC内建一个内接矩形广场DEFG(点E、F在边BC上,点D、G分别在边AB和AC上),三角形其余部分进行植被绿化,按要求欲使矩形DEFG的对角线EG最短,请在备用图中画出使对角线EG最短的矩形.并求出对角线EG的最短距离(不要求证明).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,△AOB是等腰直角三角形,∠AOB=90°,点A(2,1).
(1)求点B的坐标;
(2)求经过A、O、B三点的抛物线的函数表达式;
(3)在(2)所求的抛物线上,是否存在一点P,使四边形ABOP的面积最大?若存在,求出点P的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】孙老师在上《等可能事件的概率》这节课时,给同学们提出了一个问题:“如果同时随机投掷两枚质地均匀的骰子,它们朝上一面的点数和是多少的可能性最大?”同学们展开讨论,各抒己见,其中小芳和小超两位同学给出了两种不同的回答.小芳认为6的可能性最大,小超认为7的可能性最大.你认为他们俩的回答正确吗?请用列表或画树状图等方法加以说明.(骰子:六个面上分别刻有1,2,3,4,5,6个小圆点的小正方体.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】上周六上午
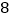 点,小颖同爸爸妈妈一起从西安出发回安康看望姥姥,途中他们在一个服务区休息了半小时,然后直达姥姥家,如图,是小颖一家这次行程中距姥姥家的距离
点,小颖同爸爸妈妈一起从西安出发回安康看望姥姥,途中他们在一个服务区休息了半小时,然后直达姥姥家,如图,是小颖一家这次行程中距姥姥家的距离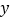 (千米)与他们路途所用的时间
(千米)与他们路途所用的时间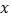 (时)之间的函数图象,请根据以上信息,解答下列问题:
(时)之间的函数图象,请根据以上信息,解答下列问题:(1)求直线
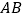 所对应的函数关系式;
所对应的函数关系式;(2)已知小颖一家出服务区后,行驶
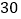 分钟时,距姥姥家还有
分钟时,距姥姥家还有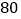 千米,问小颖一家当天几点到达姥姥家?
千米,问小颖一家当天几点到达姥姥家?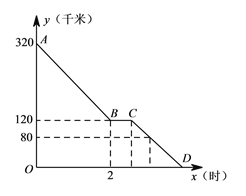
-
科目: 来源: 题型:
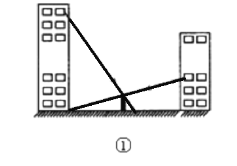
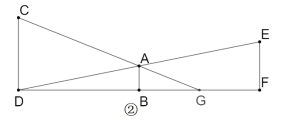
查看答案和解析>>【题目】如图,某中学两座教学楼中间有个路灯,甲、乙两个人分别在楼上观察路灯顶端,视线所及如图①所示.根据实际情况画出平面图形如图②,CD⊥DF,AB⊥DF,EF⊥DF,甲从点C可以看到点G处,乙从点E恰巧可以看到点D处,点B是DF的中点,路灯AB高5.5米,DF=120米,BG=10.5米,求甲、乙两人的观测点到地面的距离的差.
相关试题

