【题目】阅读理解:如图1,在△ABC中,当DE∥BC时可以得到三组成比例线段:① ![]() ;②
;② ![]() ;③
;③ ![]() .反之,当对应线段程比例时也可以推出DE∥BC.
.反之,当对应线段程比例时也可以推出DE∥BC.
理解运用:三角形的内接四边形是指顶点在三角形各边上的四边形.
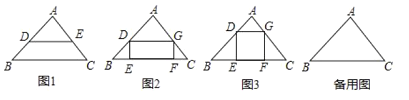
(1)如图2,已知矩形DEFG是△ABC的一个内接矩形,将矩形DEFG沿CB方向向左平移得矩形PBQH,其中顶点D、E、F、G的对应点分别为P、B、Q、H,在图2中画出平移后的图形;
(2)在(1)所得的图形中,连接CH并延长交BP的延长线于点R,连接AR.求证:AR∥BC;
(3)如图3,某小区有一块三角形空地,已知△ABC空地的边AB=400米,BC=600米,∠ABC=45°;准备在△ABC内建一个内接矩形广场DEFG(点E、F在边BC上,点D、G分别在边AB和AC上),三角形其余部分进行植被绿化,按要求欲使矩形DEFG的对角线EG最短,请在备用图中画出使对角线EG最短的矩形.并求出对角线EG的最短距离(不要求证明).
参考答案:
【答案】(1)见解析;(2)见解析;(3)图形见解析,最短距离为![]()
【解析】
(1)根据题意,利用平移的性质画出矩形PBQH即可;
(2)如图1中,连接CH并延长交BP的延长线于点R,连接AR,利用平行线分线段成比例,由PH∥BC,DG∥BC,可得对应线段成比例,再由PH=DG可证RH,BC,AG,AC四条线段对应成比例,可得到AR∥GH,再由HG∥BC,利用平行线的传递性,可证得结论;
(3)如图2中,作AR∥BC.BR⊥BC,连接CR,作BH⊥CR,过点H作PH∥BC交RB于P交AB于D交AC于G,作HQ⊥BC于Q,DE⊥BC于E,GF⊥BC于F ,易得到四边形DEFG是矩形,此时矩形的对角线最短即就是EG的长,利用勾股定理求出GR的长,再求出BH的长,然后利用平行四边形的对边相等,可求出EG的长.
(1)解:矩形PBQH如图1所示

(2)解:如图1中,连接CH并延长交BP的延长线于点R,连接AR
∵PH∥BC,
∴ ![]()
∵DG∥BC,
∴ ![]()
∵PH=DG,
∴ ![]()
∴AR∥HG,
∵HG∥BC,
∴AR∥BC
(3)解:如图2中,作AR∥BC.BR⊥BC,连接CR,作BH⊥CR,过点H作PH∥BC交RB于P交AB于D交AC于G,作HQ⊥BC于Q,DE⊥BC于E,GF⊥BC于F
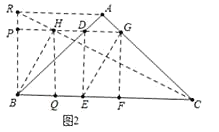
则四边形DEFG是矩形,此时矩形的对角线最短(BH是垂线段,垂线段最短,易证EG=BH,故此时矩形的对角线EG最短).
在Rt△RBC中,
∵BC=600,BR=200![]()
∴CR=![]()
∴BH=![]()
由(2)可知EG=BH=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,弦AB垂直平分半径OC,垂足为D.若点P是⊙O上异于点A,B的任意一点,则∠APB=( )
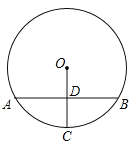
A.30°或60°B.60°或150°C.30°或150°D.60°或120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 在三边互不相等的△ABC中, D,E,F分别是AB,AC,BC边的中点.连接DE,过点C作CM∥AB交DE的延长线于点M,连接CD、EF交于点N,则图中全等三角形共有( )
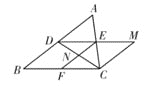
A.3对B.4对C.5对D.6对
-
科目: 来源: 题型:
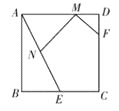
查看答案和解析>>【题目】如图,在正方形ABCD中,AB=4,E是BC边的中点, F是CD边上的一点, 且DF=1.若M、N分别是线段AD、AE上的动点,则MN+MF的最小值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,△AOB是等腰直角三角形,∠AOB=90°,点A(2,1).
(1)求点B的坐标;
(2)求经过A、O、B三点的抛物线的函数表达式;
(3)在(2)所求的抛物线上,是否存在一点P,使四边形ABOP的面积最大?若存在,求出点P的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
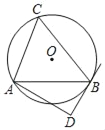
查看答案和解析>>【题目】如图,⊙O的半径为5,△ABC是⊙O的内接三角形,AB=8.AD和过点B的切线互相垂直,垂足为D.
(1)求证:∠BAD+∠C=90°;
(2)求线段AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】孙老师在上《等可能事件的概率》这节课时,给同学们提出了一个问题:“如果同时随机投掷两枚质地均匀的骰子,它们朝上一面的点数和是多少的可能性最大?”同学们展开讨论,各抒己见,其中小芳和小超两位同学给出了两种不同的回答.小芳认为6的可能性最大,小超认为7的可能性最大.你认为他们俩的回答正确吗?请用列表或画树状图等方法加以说明.(骰子:六个面上分别刻有1,2,3,4,5,6个小圆点的小正方体.)
相关试题

