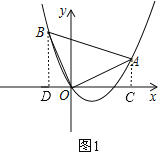
【题目】如图,在平面直角坐标系中,O为坐标原点,△AOB是等腰直角三角形,∠AOB=90°,点A(2,1).
(1)求点B的坐标;
(2)求经过A、O、B三点的抛物线的函数表达式;
(3)在(2)所求的抛物线上,是否存在一点P,使四边形ABOP的面积最大?若存在,求出点P的坐标;若不存在,请说明理由.

参考答案:
【答案】(1) B(-1.2);(2) y=![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)过A作AC⊥x轴于点C,过B作BD⊥x轴于点D,则可证明△ACO≌△ODB,则可求得OD和BD的长,可求得B点坐标;
(2)根据A、B、O三点的坐标,利用待定系数法可求得抛物线解析式;
(3)由四边形ABOP可知点P在线段AO的下方,过P作PE∥y轴交线段OA于点E,可求得直线OA解析式,设出P点坐标,则可表示出E点坐标,可表示出PE的长,进一步表示出△POA的面积,则可得到四边形ABOP的面积,再利用二次函数的性质可求得其面积最大时P点的坐标.
(1)如图1,过A作AC⊥x轴于点C,过B作BD⊥x轴于点D,
∵△AOB为等腰三角形,
∴AO=BO,
∵∠AOB=90°,
∴∠AOC+∠DOB=∠DOB+∠OBD=90°,
∴∠AOC=∠OBD,
在△ACO和△ODB中
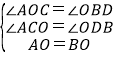
∴△ACO≌△ODB(AAS),
∵A(2,1),
∴OD=AC=1,BD=OC=2,
∴B(-1,2);
(2)∵抛物线过O点,
∴可设抛物线解析式为y=ax2+bx,
把A、B两点坐标代入可得![]() ,解得
,解得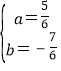 ,
,
∴经过A、B、O原点的抛物线解析式为y=![]() x2-
x2-![]() x;
x;
(3)∵四边形ABOP,
∴可知点P在线段OA的下方,
过P作PE∥y轴交AO于点E,如图2,

设直线AO解析式为y=kx,
∵A(2,1),
∴k=![]() ,
,
∴直线AO解析式为y=![]() x,
x,
设P点坐标为(t,![]() t2-
t2-![]() t),则E(t,
t),则E(t,![]() t),
t),
∴PE=![]() t-(
t-(![]() t2-
t2-![]() t)=-
t)=-![]() t2+
t2+![]() t=-
t=-![]() (t-1)2+
(t-1)2+![]() ,
,
∴S△AOP=![]() PE×2=PE═-
PE×2=PE═-![]() (t-1)2+
(t-1)2+![]() ,
,
由A(2,1)可求得OA=OB=![]() ,
,
∴S△AOB=![]() AOBO=
AOBO=![]() ,
,
∴S四边形ABOP=S△AOB+S△AOP=-![]() (t-1)2+
(t-1)2+![]() +
+![]() =
=![]() ,
,
∵-![]() <0,
<0,
∴当t=1时,四边形ABOP的面积最大,此时P点坐标为(1,-![]() ),
),
综上可知存在使四边形ABOP的面积最大的点P,其坐标为(1,-![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 在三边互不相等的△ABC中, D,E,F分别是AB,AC,BC边的中点.连接DE,过点C作CM∥AB交DE的延长线于点M,连接CD、EF交于点N,则图中全等三角形共有( )
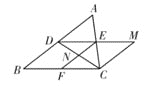
A.3对B.4对C.5对D.6对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AB=4,E是BC边的中点, F是CD边上的一点, 且DF=1.若M、N分别是线段AD、AE上的动点,则MN+MF的最小值为________.
-
科目: 来源: 题型:
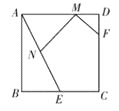
查看答案和解析>>【题目】阅读理解:如图1,在△ABC中,当DE∥BC时可以得到三组成比例线段:①
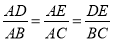 ;②
;② 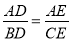 ;③
;③ 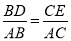 .反之,当对应线段程比例时也可以推出DE∥BC.
.反之,当对应线段程比例时也可以推出DE∥BC.理解运用:三角形的内接四边形是指顶点在三角形各边上的四边形.
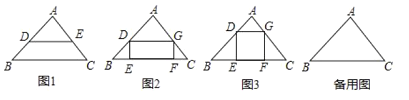
(1)如图2,已知矩形DEFG是△ABC的一个内接矩形,将矩形DEFG沿CB方向向左平移得矩形PBQH,其中顶点D、E、F、G的对应点分别为P、B、Q、H,在图2中画出平移后的图形;
(2)在(1)所得的图形中,连接CH并延长交BP的延长线于点R,连接AR.求证:AR∥BC;
(3)如图3,某小区有一块三角形空地,已知△ABC空地的边AB=400米,BC=600米,∠ABC=45°;准备在△ABC内建一个内接矩形广场DEFG(点E、F在边BC上,点D、G分别在边AB和AC上),三角形其余部分进行植被绿化,按要求欲使矩形DEFG的对角线EG最短,请在备用图中画出使对角线EG最短的矩形.并求出对角线EG的最短距离(不要求证明).
-
科目: 来源: 题型:
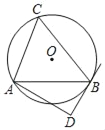
查看答案和解析>>【题目】如图,⊙O的半径为5,△ABC是⊙O的内接三角形,AB=8.AD和过点B的切线互相垂直,垂足为D.
(1)求证:∠BAD+∠C=90°;
(2)求线段AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】孙老师在上《等可能事件的概率》这节课时,给同学们提出了一个问题:“如果同时随机投掷两枚质地均匀的骰子,它们朝上一面的点数和是多少的可能性最大?”同学们展开讨论,各抒己见,其中小芳和小超两位同学给出了两种不同的回答.小芳认为6的可能性最大,小超认为7的可能性最大.你认为他们俩的回答正确吗?请用列表或画树状图等方法加以说明.(骰子:六个面上分别刻有1,2,3,4,5,6个小圆点的小正方体.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】上周六上午
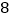 点,小颖同爸爸妈妈一起从西安出发回安康看望姥姥,途中他们在一个服务区休息了半小时,然后直达姥姥家,如图,是小颖一家这次行程中距姥姥家的距离
点,小颖同爸爸妈妈一起从西安出发回安康看望姥姥,途中他们在一个服务区休息了半小时,然后直达姥姥家,如图,是小颖一家这次行程中距姥姥家的距离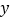 (千米)与他们路途所用的时间
(千米)与他们路途所用的时间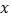 (时)之间的函数图象,请根据以上信息,解答下列问题:
(时)之间的函数图象,请根据以上信息,解答下列问题:(1)求直线
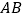 所对应的函数关系式;
所对应的函数关系式;(2)已知小颖一家出服务区后,行驶
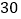 分钟时,距姥姥家还有
分钟时,距姥姥家还有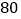 千米,问小颖一家当天几点到达姥姥家?
千米,问小颖一家当天几点到达姥姥家?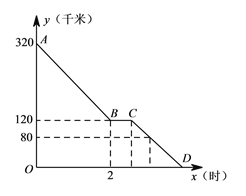
相关试题

