【题目】已知:点![]() 、
、![]() 、
、![]() 不在同一条直线上,
不在同一条直线上,![]() .
.


(1)如图1,当![]() ,
,![]() 时,求
时,求![]() 的度数;
的度数;
(2)如图2,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的平分线所在直线,试探究
的平分线所在直线,试探究![]() 与
与![]() 的数量关系;
的数量关系;
(3)如图3,在(2)的前提下,有![]() ,
,![]() ,直接写出
,直接写出![]() 的值.
的值.
参考答案:
【答案】(1)∠ACB=120°;(2)2∠AQB+∠C=180°;(3)∠DAC:∠ACB:∠CBE=1:2:2.
【解析】
(1)首先过C作AD的平行线CE,再根据平行的性质计算即可.
(2)首先过点Q作QM∥AD,再根据已知平行线的性质即可,计算的2∠AQB+∠C=180°.
(3)根据平行线的性质和角平分线的性质首先计算出∠DAC、∠ACB、∠CBE,再根据角的度数求比值.
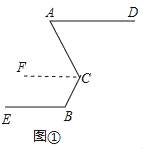
(1)在图①中,过点C作CF∥AD,则CF∥BE.
∵CF∥AD∥BE,
∴∠ACF=∠A,∠BCF=180°﹣∠B,
∴∠ACB=∠ACF+∠BCF=180°﹣(∠B﹣∠A)=120°.
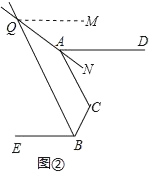
(2)在图2中,过点Q作QM∥AD,则QM∥BE.
∵QM∥AD,QM∥BE,
∴∠AQM=∠NAD,∠BQM=∠EBQ.
∵AQ平分∠CAD,BQ平分∠CBE,
∴∠NAD=![]() ∠CAD,∠EBQ=
∠CAD,∠EBQ=![]() ∠CBE,
∠CBE,
∴∠AQB=∠BQM﹣∠AQM=![]() (∠CBE﹣∠CAD).
(∠CBE﹣∠CAD).
∵∠C=180°﹣(∠CBE﹣∠CAD)=180°﹣2∠AQB,
∴2∠AQB+∠C=180°.
(3)∵AC∥QB,
∴∠AQB=∠CAP=![]() ∠CAD,∠ACP=∠PBQ=
∠CAD,∠ACP=∠PBQ=![]() ∠CBE,
∠CBE,
∴∠ACB=180°﹣∠ACP=180°﹣![]() ∠CBE.
∠CBE.
∵2∠AQB+∠ACB=180°,
∴∠CAD=![]() ∠CBE.
∠CBE.
又∵QP⊥PB,
∴∠CAP+∠ACP=90°,即∠CAD+∠CBE=180°,
∴∠CAD=60°,∠CBE=120°,
∴∠ACB=180°﹣(∠CBE﹣∠CAD)=120°,
∴∠DAC:∠ACB:∠CBE=60°:120°:120°=1:2:2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为奖励优秀学生,某校准备购买一批文具袋和圆规作为奖品,已知购买1个文具袋和2个圆规需21元,购买2个文具袋和3个圆规需39元。
(1)求文具袋和圆规的单价。
(2)学校准备购买文具袋20个,圆规若干,文具店给出两种优惠方案:
方案一:购买一个文具袋还送1个圆规。
方案二:购买圆规10个以上时,超出10个的部分按原价的八折优惠,文具袋不打折.
①设购买面规m个,则选择方案一的总费用为______,选择方案二的总费用为______.
②若学校购买圆规100个,则选择哪种方案更合算?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①b+2a=0;②abc>0;③a﹣2b+4c<0;④8a+c>0.其中正确的有( )个.
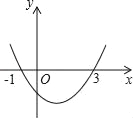
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】老师在讲完乘法公式
 的多种运用后,要求同学们运用所学知识解答:求代数式
的多种运用后,要求同学们运用所学知识解答:求代数式 的最小值?同学们经过交流、讨论,最后总结出如下解答方法:
的最小值?同学们经过交流、讨论,最后总结出如下解答方法:解:

∵
 ,
,当
 时,
时, 的值最小,最小值是0,
的值最小,最小值是0,∴

当
 时,
时, 的值最小,最小值是1,
的值最小,最小值是1,∴
 的最小值是1.
的最小值是1.请你根据上述方法,解答下列各题
(1)当x=______时,代数式
 的最小值是______;
的最小值是______;(2)若
 ,当x=______时,y有最______值(填“大”或“小”),这个值是______;
,当x=______时,y有最______值(填“大”或“小”),这个值是______;(3)若
 ,求
,求 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明.
已知:如图,
 ,
, .
.求证:
 .
.证明:∵
 ,
,∴
 __________(_______________________________________).
__________(_______________________________________).∴
 (_____________________________________________).
(_____________________________________________).∵
 ,
,∴_______

∴
 (______________________________________).
(______________________________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在菱形ABCD中,E是AB上一点,线段DE与菱形对角线AC交于点F,点O是AC的中点,EO的延长线交边DC于点G
(1)求证:∠AED=∠FBC;
(2)求证:四边形DEBG是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,《政府工作报告》中不断提出了很多新的词汇,为了解学生们对新词汇的关注度,某数学兴趣小组选取其中的
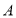 :“互联网+政务服务”,
:“互联网+政务服务”, :“工匠精神”,
:“工匠精神”, :“光网城市”,
:“光网城市”, :“大众旅游时代”四个热词在全校学生中进行了抽样调查,要求被调查的每位同学只能从中选择一个我最关注的热词,根据调查结果,该小组绘制了如下的两幅不完整的统计图:请根据统计图提供的信息,解答下列问题:
:“大众旅游时代”四个热词在全校学生中进行了抽样调查,要求被调查的每位同学只能从中选择一个我最关注的热词,根据调查结果,该小组绘制了如下的两幅不完整的统计图:请根据统计图提供的信息,解答下列问题:

(1)本次一共调查了多少名同学?
(2)求出统计图中
 ,
, 的值;
的值;(3)扇形统计图中,热词
 、
、 所在扇形统计图的圆心角分别是多少度?
所在扇形统计图的圆心角分别是多少度?
相关试题

