【题目】已知:如图,在菱形ABCD中,E是AB上一点,线段DE与菱形对角线AC交于点F,点O是AC的中点,EO的延长线交边DC于点G
(1)求证:∠AED=∠FBC;
(2)求证:四边形DEBG是平行四边形.

参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)首先证明△CBF≌△CDF,从而得到∠FBC=∠FDC,然后由平行线的性质可知∠FDC=∠AED,从而可证得∠AED=∠FBC;
(2)连接BD,由菱形的性质可知;OB=OD,然后再证明OG=OE,从而可证得四边形DEBG是平行四边形.
(1)∵四边形ABCD是菱形,
∴∠DCF=∠BCF,DC=BC.
在△DCF和△BCF中,
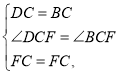
∴△DCF≌△BCF,
∴∠FBC=∠FDC.
∵DC∥AB,
∴∠FDC=∠AED.
∴∠AED=∠FBC.
(2)如图,连接BD.
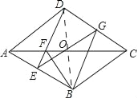
∵四边形ABCD是菱形,O是AC的中点,
∴OD=OB.
∵DC∥AB,
∴∠GCO=∠EAO.
在△GCO和△EAO中,
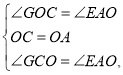
∴△GCO≌△EAO,
∴OE=OG.
∴四边形DEBG是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】老师在讲完乘法公式
 的多种运用后,要求同学们运用所学知识解答:求代数式
的多种运用后,要求同学们运用所学知识解答:求代数式 的最小值?同学们经过交流、讨论,最后总结出如下解答方法:
的最小值?同学们经过交流、讨论,最后总结出如下解答方法:解:

∵
 ,
,当
 时,
时, 的值最小,最小值是0,
的值最小,最小值是0,∴

当
 时,
时, 的值最小,最小值是1,
的值最小,最小值是1,∴
 的最小值是1.
的最小值是1.请你根据上述方法,解答下列各题
(1)当x=______时,代数式
 的最小值是______;
的最小值是______;(2)若
 ,当x=______时,y有最______值(填“大”或“小”),这个值是______;
,当x=______时,y有最______值(填“大”或“小”),这个值是______;(3)若
 ,求
,求 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点
 、
、 、
、 不在同一条直线上,
不在同一条直线上, .
.

(1)如图1,当
 ,
, 时,求
时,求 的度数;
的度数;(2)如图2,
 、
、 分别为
分别为 、
、 的平分线所在直线,试探究
的平分线所在直线,试探究 与
与 的数量关系;
的数量关系;(3)如图3,在(2)的前提下,有
 ,
, ,直接写出
,直接写出 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明.
已知:如图,
 ,
, .
.求证:
 .
.证明:∵
 ,
,∴
 __________(_______________________________________).
__________(_______________________________________).∴
 (_____________________________________________).
(_____________________________________________).∵
 ,
,∴_______

∴
 (______________________________________).
(______________________________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,《政府工作报告》中不断提出了很多新的词汇,为了解学生们对新词汇的关注度,某数学兴趣小组选取其中的
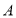 :“互联网+政务服务”,
:“互联网+政务服务”, :“工匠精神”,
:“工匠精神”, :“光网城市”,
:“光网城市”, :“大众旅游时代”四个热词在全校学生中进行了抽样调查,要求被调查的每位同学只能从中选择一个我最关注的热词,根据调查结果,该小组绘制了如下的两幅不完整的统计图:请根据统计图提供的信息,解答下列问题:
:“大众旅游时代”四个热词在全校学生中进行了抽样调查,要求被调查的每位同学只能从中选择一个我最关注的热词,根据调查结果,该小组绘制了如下的两幅不完整的统计图:请根据统计图提供的信息,解答下列问题:

(1)本次一共调查了多少名同学?
(2)求出统计图中
 ,
, 的值;
的值;(3)扇形统计图中,热词
 、
、 所在扇形统计图的圆心角分别是多少度?
所在扇形统计图的圆心角分别是多少度? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,点E,F分别在BC,AB上,点M在BA的延长线上,且CE=BF=AM,过点M,E分别作NM⊥DM,NE⊥DE交于N,连接NF.
(1)求证:DE⊥DM;
(2)猜想并写出四边形CENF是怎样的特殊四边形,并证明你的猜想.

-
科目: 来源: 题型:
查看答案和解析>>【题目】据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m).
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.

相关试题

