【题目】在平面直角坐标系中,如图1,将n个边长为1的正方形并排组成矩形OABC,相邻两边OA和OC分别落在x轴和y轴的正半轴上,设抛物线y=ax2+bx+c(a<0)过矩形顶点B、C. 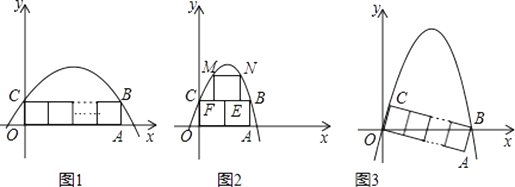
(1)当n=1时,如果a=﹣1,试求b的值;
(2)当n=2时,如图2,在矩形OABC上方作一边长为1的正方形EFMN,使EF在线段CB上,如果M,N两点也在抛物线上,求出此时抛物线的解析式;
(3)将矩形OABC绕点O顺时针旋转,使得点B落到x轴的正半轴上,如果该抛物线同时经过原点O. ①试求当n=3时a的值;
②直接写出a关于n的关系式.
参考答案:
【答案】
(1)解:∵抛物线过矩形顶点B、C,其中C(0,1),B(n,1)
∴当n=1时,抛物线对称轴为直线x= ![]() ,
,
∴ ![]() ,
,
∵a=﹣1,
∴b=1,
答:b的值是1
(2)解:设所求抛物线解析式为y=ax2+bx+1,
由对称性可知抛物线经过点B(2,1)和点M( ![]() ,2),
,2),
则 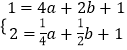 ,
,
解得 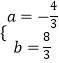
∴所求抛物线解析式为 ![]() ,
,
答:此时抛物线的解析式是 ![]()
(3)解:①当n=3时,OC=1,BC=3,
设所求抛物线解析式为y=ax2+bx,
过C作CD⊥OB于点D,
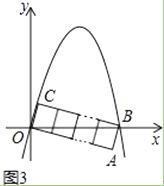
则Rt△OCD∽Rt△OBC,
∴ ![]() ,
,
设OD=t,则CD=3t,
∵OD2+CD2=OC2,
∴(3t)2+t2=12,
∴ ![]() ,
,
∴C( ![]() ,
, ![]() ),
),
又∵B( ![]() ,0),
,0),
∴把B、C坐标代入抛物线解析式,得 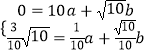 ,
,
解得:a=﹣ ![]() ,
,
a关于n的关系式是 ![]()
【解析】(1)根据已知得到抛物线对称轴为直线x= ![]() ,代入即可求出b;(2)设所求抛物线解析式为y=ax2+bx+1,由对称性可知抛物线经过点B(2,1)和点M(
,代入即可求出b;(2)设所求抛物线解析式为y=ax2+bx+1,由对称性可知抛物线经过点B(2,1)和点M( ![]() ,2),把B、M的坐标代入得到方程组
,2),把B、M的坐标代入得到方程组 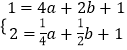 ,求出a、b的值即可得到抛物线解析式;(3)①当n=3时,OC=1,BC=3,设所求抛物线解析式为y=ax2+bx,过C作CD⊥OB于点D,则Rt△OCD∽Rt△OBC,得出
,求出a、b的值即可得到抛物线解析式;(3)①当n=3时,OC=1,BC=3,设所求抛物线解析式为y=ax2+bx,过C作CD⊥OB于点D,则Rt△OCD∽Rt△OBC,得出 ![]() ,设OD=t,则CD=3t,根据勾股定理OD2+CD2=OC2 , 求出t,得出C的坐标,把B、C坐标代入抛物线解析式即可得到方程组,求出a即可;②根据(1)、(2)①总结得到答案.
,设OD=t,则CD=3t,根据勾股定理OD2+CD2=OC2 , 求出t,得出C的坐标,把B、C坐标代入抛物线解析式即可得到方程组,求出a即可;②根据(1)、(2)①总结得到答案.
【考点精析】根据题目的已知条件,利用解二元一次方程组和勾股定理的概念的相关知识可以得到问题的答案,需要掌握二元一次方程组:①代入消元法;②加减消元法;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班师生组织植树活动,上午8时从学校出发,到植树地点植树后原路返校,如图为师生离校路程s与时间t之间的图象.请回答下列问题:
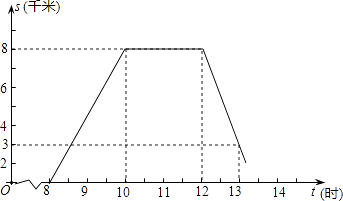
(1)求师生何时回到学校?
(2)如果运送树苗的三轮车比师生迟半小时出发,与师生同路匀速前进,早半小时到达植树地点,请在图中,画出该三轮车运送树苗时,离校路程s与时间t之间的图象,并结合图象直接写出三轮车追上师生时,离学校的路程;
(3)如果师生骑自行车上午8时出发,到植树地点后,植树需2小时,要求14时前返回到学校,往返平均速度分别为每时10km、8km.现有A、B、C、D四个植树点与学校的路程分别是13km、15km、17km、19km,试通过计算说明哪几个植树点符合要求. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)﹣
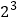 ﹣[(﹣3) ﹣2×
﹣[(﹣3) ﹣2× 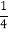 ﹣8.5]÷(﹣
﹣8.5]÷(﹣  )
) (2)
 ×
×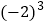 ﹣0.25×(﹣4)×(﹣3);
﹣0.25×(﹣4)×(﹣3);(3)(﹣1
 )﹣1
)﹣1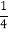 +(﹣
+(﹣  )﹣3
)﹣3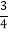 ﹣(﹣1
﹣(﹣1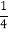 )
)(4)
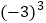 ÷4
÷4  ×(﹣
×(﹣ )+5﹣2×(﹣
)+5﹣2×(﹣  )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程: (1)x﹣3=-2x+1 (2)18(x-1)=-2(2x﹣1)(3)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(1,3)、点B(m,1)是一次函数
 的图像上的两点,一次函数
的图像上的两点,一次函数 图像与x轴交于点D.
图像与x轴交于点D.
(1)b = ,m = ;
(2)过点B作直线l垂直于x轴,点E是点D关于直线l的对称点,点C是点A关于原点的对称点.试判断点B、E、C是否在同一条直线上,并说明理由.
(3)连结AO、BO,求△AOB的面积;
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人相约元旦登山,甲、乙两人距地面的高度y(m)与登山时间x(min)之间的函数图像如图所示,根据图像所提供的信息解答下列问题:
(1)t= min.
(2)若乙提速后,乙登山的上升速度是甲登山的上升速度3倍,
①则甲登山的的上升速度是 m/min;
②请求出甲登山过程中,距地面的高度y(m)与登山时间x(min)之间的函数关系式.
③当甲、乙两人距地面高度差为70m时,求x的值(直接写出满足条件的x值).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆C,点B是该半圆周上一动点,连接OB、AB,并延长AB至点D,使DB=AB,过点D作x轴垂线,分别交x轴、直线OB于点E、F,点E为垂足,连接CF.
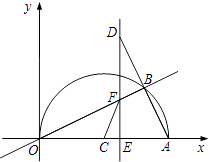
(1)当∠AOB=30°时,求弧AB的长度;
(2)当DE=8时,求线段EF的长;
(3)在点B运动过程中,是否存在以点E、C、F为顶点的三角形与△AOB相似?若存在,请求出此时点E的坐标;若不存在,请说明理由.
相关试题

