【题目】甲、乙两人相约元旦登山,甲、乙两人距地面的高度y(m)与登山时间x(min)之间的函数图像如图所示,根据图像所提供的信息解答下列问题:
(1)t= min.
(2)若乙提速后,乙登山的上升速度是甲登山的上升速度3倍,
①则甲登山的的上升速度是 m/min;
②请求出甲登山过程中,距地面的高度y(m)与登山时间x(min)之间的函数关系式.
③当甲、乙两人距地面高度差为70m时,求x的值(直接写出满足条件的x值).

参考答案:
【答案】(1)t=2min;(2)①甲登山上升的速度是10m/min;y=10x+100(0≤x≤20);x=3,10,13
【解析】试题分析:(1)根据速度=高度÷时间即可算出甲登山上升的速度,即可算出乙在A地时所用的时间![]()
![]() ①求得乙提速后乙的速度,根据乙登山的上升速度是甲登山的上升速度3倍,即可求得甲的速度.
①求得乙提速后乙的速度,根据乙登山的上升速度是甲登山的上升速度3倍,即可求得甲的速度.
②找出甲登山全程中y关于x的函数关系式.
③分![]() 和
和![]() 两种情况,根据高度=初始高度+速度×时间即可得出乙登上过程中y关于x的函数关系;令二者做差等于70即可得出关于x的一元一次方程,解之即可得出结论.
两种情况,根据高度=初始高度+速度×时间即可得出乙登上过程中y关于x的函数关系;令二者做差等于70即可得出关于x的一元一次方程,解之即可得出结论.
试题解析:
(1)![]() 解得:
解得: ![]()
故答案为:2.
(2)①乙提速后,乙的登上速度为: ![]()
乙提速后,乙登山的上升速度是甲登山的上升速度3倍,
甲登山上升的速度是10m/min;
故答案为:10.
∵甲登山上升的速度是10m/min,
∴甲登山所用的时间为20min.
即点![]()
由图像可知点![]()
设直线CD的函数关系式: ![]()
③当![]() 时,
时, ![]()
![]() 时,y=30+10×3(x2)=30x30.
时,y=30+10×3(x2)=30x30.
∴乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为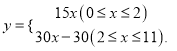
(3)当10x+100(30x30)=70时,解得:x=3;
当30x30(10x+100)=70时,解得:x=10.
当![]() 时,解得:x=13.
时,解得:x=13.
答:登山3分钟或10分钟或13分钟时,甲、乙两人距地面的高度差为70米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(1,3)、点B(m,1)是一次函数
 的图像上的两点,一次函数
的图像上的两点,一次函数 图像与x轴交于点D.
图像与x轴交于点D.
(1)b = ,m = ;
(2)过点B作直线l垂直于x轴,点E是点D关于直线l的对称点,点C是点A关于原点的对称点.试判断点B、E、C是否在同一条直线上,并说明理由.
(3)连结AO、BO,求△AOB的面积;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在方格纸中(小正方形的边长为1),△ABC的三个顶点均为格点,将△ABC沿x轴向左平移5个单位长度,根据所给的直角坐标系(O是坐标原点),解答下列问题:

(1)画出平移后的△A′B′C′,并直接写出点A′、B′、C′的坐标;
(2)求出在整个平移过程中,△ABC扫过的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,AC=BC=2,正方形CDEF的顶点D、F分别在AC、BC边上,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象中能表示y与x之间的函数关系的是( )
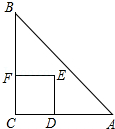
A.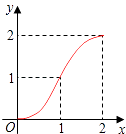
B.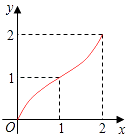
C.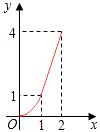
D.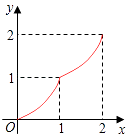
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标中表示下面各点:A(0,3),B(1,﹣3),C(3,﹣5),D(﹣3,﹣5),E(3,5),F(5,7).
①A点到原点O的距离是________ .
②将点C向x轴的负方向平移6个单位它与点________重合.
③连接CE,则直线CE与y轴位置关系是________ .
④点F分别到x、y轴的距离分别是________ .

-
科目: 来源: 题型:
查看答案和解析>>【题目】同庆中学为丰富学生的校园生活,准备从军跃体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元.
(1)购买一个足球、一个篮球各需多少元?
(2)根据同庆中学的实际情况,需从军跃体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一直径是
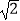 米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,则:
米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,则: 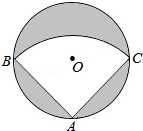
(1)AB的长为米;
(2)用该扇形铁皮围成一个圆锥,所得圆锥的底面圆的半径为米.
相关试题

