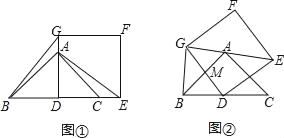
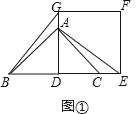
【题目】如图①,AD为等腰直角△ABC的高,点A和点C分别在正方形DEFG的边DG和DE上,连接BG、AE.
(1)求证:BG=AE;
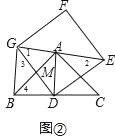
(2)将正方形DEFG绕点D旋转,当线段EG经过点A时,(如图②所示)
①求证:BG⊥GE;
②设DG与AB交于点M,若AG=6,AE=8,求DM的长.
参考答案:
【答案】(1)证明见解析;(2)①证明见解析;②DM=![]() ,
,
【解析】试题分析:(1)如图①,根据等腰直角三角形的性质得AD=BD,再根据正方形的性质得∠GDE=90°,DG=DE,则可根据“SAS“判断△BDG≌△ADE,于是得到BG=AE;
(2)①如图②,先判断△DEG为等腰直角三角形得到∠1=∠2=45°,再由△BDG≌△ADE得到∠3=∠2=45°,则可得∠BGE=90°,所以BG⊥GE;
②由AG=6,则AE=8,即GE=14,利用等腰直角三角形的性质得DG=![]() GE=7
GE=7![]() ,由(1)的结论得BG=AE=8,则根据勾股定理得AB=10,接着由△ABD为等腰直角三角形得到∠4=45°,BD=
,由(1)的结论得BG=AE=8,则根据勾股定理得AB=10,接着由△ABD为等腰直角三角形得到∠4=45°,BD=![]() AB=5
AB=5![]() ,然后证明△DBM∽△DGB,则利用相似比可计算出DM;
,然后证明△DBM∽△DGB,则利用相似比可计算出DM;
试题解析:
(1)证明:如图①,
∵AD为等腰直角△ABC的高,
∴AD=BD,
∵四边形DEFG为正方形,
∴∠GDE=90°,DG=DE,
在△BDG和△ADE中
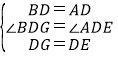 ,
,
∴△BDG≌△ADE,
∴BG=AE;
(2)①证明:如图②,
∵四边形DEFG为正方形,
∴△DEG为等腰直角三角形,
∴∠1=∠2=45°,
由(1)得△BDG≌△ADE,
∴∠3=∠2=45°,
∴∠1+∠3=45°+45°=90°,即∠BGE=90°,
∴BG⊥GE;
②解:∵AG=6,则AE=8,即GE=14,
∴DG=![]() GE=7
GE=7![]() ,
,
∵△BDG≌△ADE,
∴BG=AE=8,
在Rt△BGA中,AB=![]() =10,
=10,
∵△ABD为等腰直角三角形,
∴∠4=45°,BD=![]() AB=5
AB=5![]() ,
,
∴∠3=∠4,
而∠BDM=∠GDB,
∴△DBM∽△DGB,
∴BD:DG=DM:BD,即 5![]() :7
:7![]() =DM:5
=DM:5![]() ,
,
∴DM=![]() ,
,
-
科目: 来源: 题型:
查看答案和解析>>【题目】在大课间活动中,同学们积极参加体育锻炼,小明就本班同学“我最喜爱的体育项目”进行了一次调查统计,下面是他通过收集数据后,绘制的两幅不完整的统计图(图1,图2).请你根据图中提供的信息,解答以下问题:

(1)该班共有 名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“乒乓球”部分所对应的圆心角度数为 ;
(4)若全校有2000名学生,则“其他”部分的学生人数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某数学兴趣小组在活动课上测量学校旗杆的高度.已知小亮站着测量,眼睛与地面的距离(AB)是1.7米,看旗杆顶部E的仰角为30°;小敏蹲着测量,眼睛与地面的距离(CD)是0.7米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).
(1)求小敏到旗杆的距离DF.(结果保留根号)
(2)求旗杆EF的高度.(结果保留整数,参考数据:
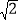 ≈1.4,
≈1.4,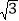 ≈1.7)
≈1.7)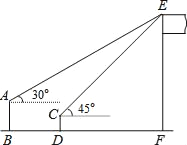
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2)、B(0,4)、C(0,2),
(1)画出△ABC关于点C成中心对称的△A1B1C;
(2)平移△ABC:若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(3)△A1B1C和△A2B2C2关于某一点成中心对称,则对称中心的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级的三位老师带部分学生去红色旅游,联系了甲、乙两家旅行社,甲旅行社说:“带队老师免费,学生可以打8折.”乙旅行社说:“包括老师在内全部七折.”若全程费用每人200元.
(1)设有
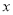 名学生参加活动,请分别写出参加两家旅行社的费用;
名学生参加活动,请分别写出参加两家旅行社的费用;(2)若有25名学生参加活动,选择哪家旅行社更合算?
(3)计算21名和15名学生参加活动时,两家旅行社的费用分别是多少?根据上面的结果应如何选择哪家旅行社更合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),B(3,0)两点,与y轴交于点C(0,﹣3).
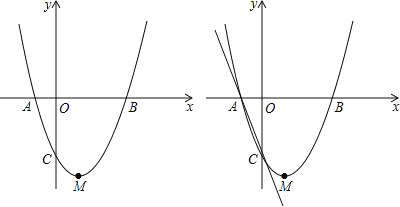
(1)求该抛物线的解析式及顶点M坐标;
(2)求△BCM面积与△ABC面积的比;
(3)若P是x轴上一个动点,过P作射线PQ∥AC交抛物线于点Q,随着P点的运动,在抛物线上是否存在这样的点Q,使以A,P,Q,C为顶点的四边形为平行四边形?若存在,请求出Q点坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是
A. “明天降雨的概率是80%”表示明天有80%的时间都在降雨
B. “抛一枚硬币正面朝上的概率为
 ”表示每抛2次就有一次正面朝上
”表示每抛2次就有一次正面朝上C. “彩票中奖的概率为1%”表示买100张彩票肯定会中奖
D. “抛一枚正方体骰子,朝上的点数为2的概率为
 ”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在 附近
附近
相关试题

