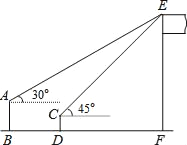
【题目】如图,某数学兴趣小组在活动课上测量学校旗杆的高度.已知小亮站着测量,眼睛与地面的距离(AB)是1.7米,看旗杆顶部E的仰角为30°;小敏蹲着测量,眼睛与地面的距离(CD)是0.7米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).
(1)求小敏到旗杆的距离DF.(结果保留根号)
(2)求旗杆EF的高度.(结果保留整数,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
参考答案:
【答案】(1)DF=(4+3![]() )米;(2)旗杆的高度约为10米.
)米;(2)旗杆的高度约为10米.
【解析】试题分析:过点A作AM⊥EF于M,过点C作CN⊥EF于N,设CN=x,则EN=x,AM=5+x,可求EM,在RtΔAEM中利用三角函数关系可求出DF的长.
(2)由EM+FM可求出EF的长.
试题解析:(1)过点A作AM⊥EF于点M,过点C作CN⊥EF于点N.设CN= x
在RtΔECN中, ∵∠ECN=45°
∴EN=CN=x
∴EM=x+0.7-1.7=x-1
∵BD=5
∴AM=BF=5+x
在RtΔAEM中, ∵∠EAM=30°
∴![]()
∴![]()
解得![]()
即DF= 4+![]() (米)
(米)
(2)EF=x +0.7="4+"![]() +0.7=4+3×1.7+0.7=9.8≈10(米)
+0.7=4+3×1.7+0.7=9.8≈10(米)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,E、F分别是AB、CD的中点,AF与DE相交于点G,CE与BF相交于点H.
(1)求证:四边形EHFG是平行四边形;
(2)□ABCD应满足什么条件时,四边形EHFG是矩形?并说明理由;
(3)□ABCD应满足什么条件时,四边形EHFG是正方形?(不要说明理由).

-
科目: 来源: 题型:
查看答案和解析>>【题目】将
 的边
的边 绕点
绕点 顺时针旋转
顺时针旋转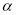 得到
得到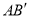 ,边
,边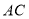 绕点
绕点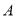 逆时针旋转
逆时针旋转 得到
得到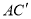 ,
,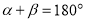 ,连接
,连接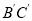 ,作
,作 的中线
的中线 .
.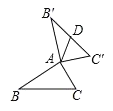
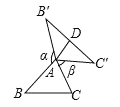

图① 图② 图③
(初步感知)
(1)如图①,当
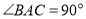 ,
,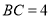 时,
时, 的长为 ;
的长为 ;(探究运用)
(2)如图②,
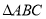 为任意三角形时,猜想
为任意三角形时,猜想 与
与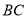 的数量关系,并证明.
的数量关系,并证明.(应用延伸)
(3)如图③,已知等腰
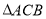 ,
,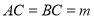 ,延长
,延长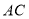 到
到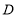 ,延长
,延长 到
到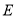 ,使
,使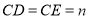 ,将
,将 绕点
绕点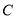 顺时针旋转一周得到
顺时针旋转一周得到 ,连接
,连接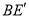 、
、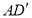 ,若
,若 ,求
,求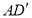 的长度(用含
的长度(用含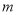 、
、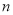 的代数式表示).
的代数式表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】在大课间活动中,同学们积极参加体育锻炼,小明就本班同学“我最喜爱的体育项目”进行了一次调查统计,下面是他通过收集数据后,绘制的两幅不完整的统计图(图1,图2).请你根据图中提供的信息,解答以下问题:

(1)该班共有 名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“乒乓球”部分所对应的圆心角度数为 ;
(4)若全校有2000名学生,则“其他”部分的学生人数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2)、B(0,4)、C(0,2),
(1)画出△ABC关于点C成中心对称的△A1B1C;
(2)平移△ABC:若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(3)△A1B1C和△A2B2C2关于某一点成中心对称,则对称中心的坐标为 .
-
科目: 来源: 题型:
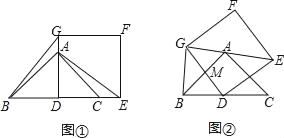
查看答案和解析>>【题目】如图①,AD为等腰直角△ABC的高,点A和点C分别在正方形DEFG的边DG和DE上,连接BG、AE.
(1)求证:BG=AE;
(2)将正方形DEFG绕点D旋转,当线段EG经过点A时,(如图②所示)
①求证:BG⊥GE;
②设DG与AB交于点M,若AG=6,AE=8,求DM的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级的三位老师带部分学生去红色旅游,联系了甲、乙两家旅行社,甲旅行社说:“带队老师免费,学生可以打8折.”乙旅行社说:“包括老师在内全部七折.”若全程费用每人200元.
(1)设有
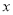 名学生参加活动,请分别写出参加两家旅行社的费用;
名学生参加活动,请分别写出参加两家旅行社的费用;(2)若有25名学生参加活动,选择哪家旅行社更合算?
(3)计算21名和15名学生参加活动时,两家旅行社的费用分别是多少?根据上面的结果应如何选择哪家旅行社更合算?
相关试题

