【题目】阅读下面的文字,解答问题:大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部写出来,而
的小数部分我们不可能全部写出来,而![]() <2于是可用
<2于是可用![]() 来表示
来表示![]() 的小数部分.请解答下列问题:
的小数部分.请解答下列问题:
(1)![]() 的整数部分是_______,小数部分是_________;
的整数部分是_______,小数部分是_________;
(2)如果![]() 的小数部分为
的小数部分为![]() 的整数部分为
的整数部分为![]() 求
求![]() 的值;
的值;
(3)已知:![]() 其中
其中![]() 是整数,且
是整数,且![]() 求
求![]() 的平方根。
的平方根。
参考答案:
【答案】(1) 4,![]() -4;(2)1;(2) ±12.
-4;(2)1;(2) ±12.
【解析】
(1)先估算出![]() 的范围,即可得出答案;
的范围,即可得出答案;
(2)先估算出![]() 、
、![]() 的范围,求出a、b的值,再代入求出即可;
的范围,求出a、b的值,再代入求出即可;
(3)先估算出![]() 的范围,求出x、y的值,再代入求出即可.
的范围,求出x、y的值,再代入求出即可.
解:(1)∵4<![]() <5,
<5,
∴![]() 的整数部分是4,小数部分是
的整数部分是4,小数部分是![]() -4,
-4,
故答案为:4,![]() -4;
-4;
(2)∵2<![]() <3,
<3,
∴a=![]() -2,
-2,
∵3<![]() <4,
<4,
∴b=3,
∴a+b-![]() =
=![]() -2+3-
-2+3-![]() =1;
=1;
(3)∵100<110<121,
∴10<![]() <11,
<11,
∴110<100+![]() <111,
<111,
∵100+![]() =x+y,其中x是整数,且0<y<1,
=x+y,其中x是整数,且0<y<1,
∴x=110,y=100+![]() -110=
-110=![]() -10,
-10,
∴x+![]() +24-y=110+
+24-y=110+![]() +24-
+24-![]() +10=144,
+10=144,
x+![]() +24-y的平方根是±12.
+24-y的平方根是±12.
-
科目: 来源: 题型:
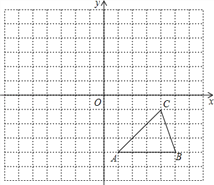
查看答案和解析>>【题目】每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,
①写出A、B、C的坐标.
②以原点O为对称中心,画出△ABC关于原点O对称的△A1B1C1,并写出A1、B1、C1的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在
 中,
中, 为锐角,点
为锐角,点 为射线
为射线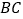 上一点,联结
上一点,联结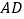 ,以
,以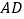 为一边且在
为一边且在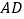 的右侧作正方形
的右侧作正方形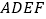 .
.(1)如果
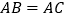 ,
,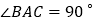 ,
,①当点
 在线段
在线段 上时(与点
上时(与点 不重合),如图2,线段
不重合),如图2,线段 所在直线的位置关系为 ,线段
所在直线的位置关系为 ,线段 的数量关系为 ;
的数量关系为 ;②当点
 在线段
在线段 的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;(2)如果
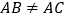 ,
,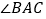 是锐角,点
是锐角,点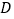 在线段
在线段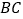 上,当
上,当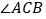 满足什么条件时,
满足什么条件时,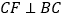 (点
(点 不重合),并说明理由.
不重合),并说明理由. 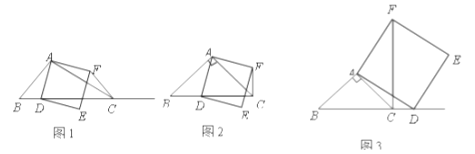
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,
 ,
, 且满足:
且满足: ,长方形
,长方形 在坐标系中(如图1),点
在坐标系中(如图1),点 为坐标系的原点.
为坐标系的原点.
(1)求点
 的坐标.
的坐标.(2)如图2,若点
 从点
从点 出发,以2个单位/秒的速度向右运动(不超过点
出发,以2个单位/秒的速度向右运动(不超过点 ),点
),点 从原点
从原点 出发,以1个单位/秒的速度向下运动(不超过点
出发,以1个单位/秒的速度向下运动(不超过点 ),设
),设 两点同时出发,在它们运动的过程中,四边形
两点同时出发,在它们运动的过程中,四边形 的面积是否发生变化?若不变,求其值;若变化,求变化的范围.
的面积是否发生变化?若不变,求其值;若变化,求变化的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF, BD=CE.

(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;
(3)△DEF可能是等腰直角三角形吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上,点
 分别表示数1、
分别表示数1、 ,则数轴上表示数
,则数轴上表示数 的点应落在______.(填“点
的点应落在______.(填“点 的左边”、“线段
的左边”、“线段 上”或“点
上”或“点 的右边”)
的右边”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下面的证明过程补充完整.
已知:如图,
 是
是 的角平分线,点
的角平分线,点 在
在 上,点
上,点 在
在 延长线上,
延长线上, 交
交 于点
于点 ,且
,且 .
.求证:
 .
.
证明:在
 中,
中, ( ).
( ).又
 (已知),
(已知),
 .
. 是
是 的角平分线,
的角平分线, ( ).
( ). (等量代换).
(等量代换). .
. ( ).
( ).
相关试题

