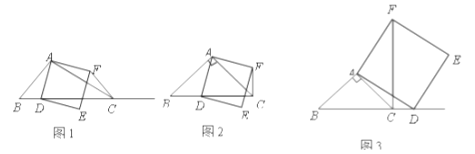
【题目】如图1,在![]() 中,
中,![]() 为锐角,点
为锐角,点![]() 为射线
为射线![]() 上一点,联结
上一点,联结![]() ,以
,以![]() 为一边且在
为一边且在![]() 的右侧作正方形
的右侧作正方形![]() .
.
(1)如果![]() ,
,![]() ,
,
①当点![]() 在线段
在线段![]() 上时(与点
上时(与点![]() 不重合),如图2,线段
不重合),如图2,线段![]() 所在直线的位置关系为 ,线段
所在直线的位置关系为 ,线段![]() 的数量关系为 ;
的数量关系为 ;
②当点![]() 在线段
在线段![]() 的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果![]() ,
,![]() 是锐角,点
是锐角,点![]() 在线段
在线段![]() 上,当
上,当![]() 满足什么条件时,
满足什么条件时,![]() (点
(点![]() 不重合),并说明理由.
不重合),并说明理由.
参考答案:
【答案】(1)①垂直,相等;②当点D在BC的延长线上时①的结论仍成立,证明见解析;(2)当∠ACB=45时,CF⊥BD,理由见解析.
【解析】试题分析:(1)①点![]() 在线段
在线段![]() 上时,根据等腰直角三角形的性质,即可得出
上时,根据等腰直角三角形的性质,即可得出![]() ②当点D在BC的延长线上时,①的结论仍成立.由正方形ADEF的性质可推出△DAB≌△FAC,所以CF=BD,∠ACF=∠ABD.结合
②当点D在BC的延长线上时,①的结论仍成立.由正方形ADEF的性质可推出△DAB≌△FAC,所以CF=BD,∠ACF=∠ABD.结合![]()
![]() 得到
得到![]() 即
即![]()
(2)当![]() 时, 过点A作AG⊥AC交CB或CB的延长线于点G,则∠GAC=
时, 过点A作AG⊥AC交CB或CB的延长线于点G,则∠GAC=![]() ,可推出
,可推出![]() 所以
所以![]() 由(1)①中的方法可得CF⊥BC.
由(1)①中的方法可得CF⊥BC.
试题解析:(1)①如图2,易证△DAB≌△FAC(SAS),
![]()
![]()
![]()
![]() 即BD⊥CF;
即BD⊥CF;
故答案为:垂直,相等;
②如图3所示,当点D在BC的延长线上时,①中的结论仍成立,
证明:由正方形ADEF得,AD=AF,∠DAF=![]() .
.
∵∠BAC=![]() ,
,
∴∠DAF=∠BAC,
∴∠DAB=∠FAC,
又∵AB=AC,
∴△DAB≌△FAC(SAS),
∴CF=BD,∠ACF=∠ABD.
∵∠BAC=![]() ,AB=AC,
,AB=AC,
![]()
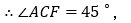
![]() ,即CF⊥BD;
,即CF⊥BD;
(2)如图4所示,当![]() 时,CF⊥BD.
时,CF⊥BD.
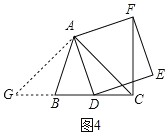
理由:过点A作AG⊥AC交CB或CB的延长线于点G,则∠GAC=![]() ,
,
![]()
∴∠ACB=∠AGC,
∴AC=AG,
又∵∠DAG=∠FAC(同角的余角相等),AD=AF,
∴△GAD≌△CAF(SAS),
![]()
![]() 即CF⊥BC.
即CF⊥BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是( )
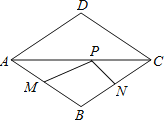
A.
 B. 1 C.
B. 1 C. 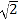 D. 2
D. 2 -
科目: 来源: 题型:
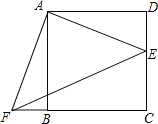
查看答案和解析>>【题目】如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置.
(1)旋转中心是点 ,旋转角度是 度;
(2)若连结EF,则△AEF是 三角形;并证明;
(3)若四边形AECF的面积为25,DE=2,求AE的长.
-
科目: 来源: 题型:
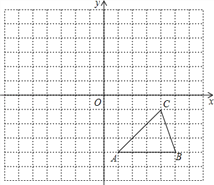
查看答案和解析>>【题目】每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,
①写出A、B、C的坐标.
②以原点O为对称中心,画出△ABC关于原点O对称的△A1B1C1,并写出A1、B1、C1的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的二次函数y=x2-(2m-1)x+m2+3m+4.
(1)探究m取不同值时,二次函数y的图象与x轴的交点的个数情况;
(2)设二次函数的图象与x轴的交点为A(x1,0),B(x2,0),且x12+x22=5,与y轴的交点为C,它的顶点为M,求直线CM的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,美丽的弦图,蕴含着四个全等的直角三角形.已知每个直角三角形较长的直角边为a,较短的直角边为b,斜边长为c.如图②,现将这四个全图②等的直角三角形紧密拼接,形成飞镖状,已知外围轮廓(实线)的周长为24,OC=3,则该飞镖状图案的面积( )
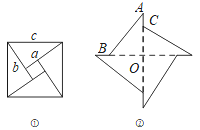
A. 6 B. 12 C. 24 D. 24
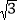
-
科目: 来源: 题型:
查看答案和解析>>【题目】使得函数值为零的自变量的值称为函数的零点.例如,对于函数y=x-1,令y=0可得x=1,我们就说1是函数y=x-1的零点.
已知y=x2-2mx-2(m+3)(m为常数).
(1)当m=0时,求该函数的零点;
(2)证明:无论m取何值,该函数总有两个零点;
(3)设函数的两个零点分别为x1和x2,且
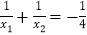 ,此时函数图象与x轴的交点分别为A,B(点A在点B左侧),点M在直线y=x-10上,当MA+MB最小时,求直线AM的函数表达式.
,此时函数图象与x轴的交点分别为A,B(点A在点B左侧),点M在直线y=x-10上,当MA+MB最小时,求直线AM的函数表达式.
相关试题

