【题目】如图,在Rt△ABC中,∠C=90°,∠A的平分线交BC于D. 过C点作CG⊥AB于G,交AD于E. 过D点作DF⊥AB于F. 下列结论:①∠CED=∠CDE;②S△AEC:S△AEG=AC:AG;③∠ADF=2∠FDB;④CE=DF.其中正确的结论有( )
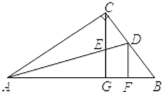
A.1个B.2个C.3个D.4个
参考答案:
【答案】C
【解析】
由∠C=90°,CG⊥AB,得∠ACE=∠B,再由外角的性质,得∠CED=∠CDE,得CE=CD;根据角平分线的性质,得CD=DF,则S△AEC:S△AEG=AC:AG;得CE=DF,从而得出答案.
∵∠ACE+∠BCG=90°,∠B+∠BCG=90°
∴∠ACE=∠B
∵∠CED=∠CAE+∠ACE,∠CDE=∠B+∠DA
∴∠CED=∠CDE,故①正确;
∴CE=CD
又AE平分∠CAB
∴CD=DF
∴CE=DF,故④正确;
过E作EH垂直于AC由角平线性质得EH=EG
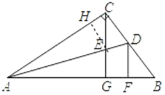
可得S△AEC:S△AEG=![]() ACEH:
ACEH:![]() AGEG=AC:AG;故②正确;
AGEG=AC:AG;故②正确;
无法证明∠ADF=2∠FDB,故④错误.
∴正确的结论有3个.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)如图,直线AB,CD相交于点O,OE⊥CD于点O,OD平分∠BOF,∠BOE=50
 ,
,求∠AOC,∠AOF,∠EOF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形ABCD是平行四边形,点A、B在x轴上,点C、D在第二象限,点M是BC中点.已知AB=6,AD=8,∠DAB=60°,点B的坐标为(-6,0).
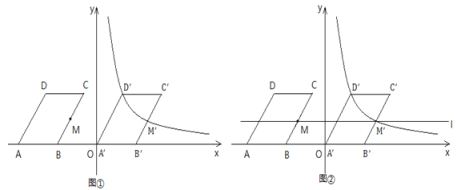
(1)求点D和点M的坐标;
(2)如图①,将□ABCD沿着x轴向右平移a个单位长度,点D的对应点
 和点M的对应点
和点M的对应点 恰好在反比例函数
恰好在反比例函数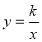 (x>0)的图像上,请求出a的值以及这个反比例函数的表达式;
(x>0)的图像上,请求出a的值以及这个反比例函数的表达式;(3)如图②,在(2)的条件下,过点M,
 作直线l,点P是直线l上的动点,点Q是平面内任意一点,若以
作直线l,点P是直线l上的动点,点Q是平面内任意一点,若以 ,P、Q为顶点的四边形是矩形,请直接写出所有满足条件的点Q的坐标.
,P、Q为顶点的四边形是矩形,请直接写出所有满足条件的点Q的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2-(k+2)x+2k=0.
(1)求证:k取任何实数值,方程总有实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,CE平分∠ACB,交AB于点E.
(1)求证:AC平分∠DAB;
(2)求证:△PCE是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等边三角形,AE=CD,AD交BE于点P,BQ⊥AD于Q.
(1)求证:AD=BE;
(2)设∠BPQ=α,那么α的大小是否随D、E的位置变化而变化?请说明理由;
(3)若PQ=3,PE=1,求AD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D在AC上,点F、G分别在AC、BC的延长线上,CE平分∠ACB交BD于点O,且∠EOD+∠OBF=180°,∠F=∠G.则图中与∠ECB相等的角有( )
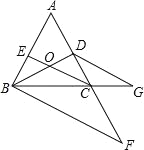
A. 6个 B. 5个 C. 4个 D. 3个
相关试题

