Question

【题目】如图，AB是⊙O的直径，点C是⊙O上一点，AD与过点C的切线垂直，垂足为点D，直线DC与AB的延长线相交于点P，CE平分∠ACB，交AB于点E．

（1）求证：AC平分∠DAB；

（2）求证：△PCE是等腰三角形.

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】（1）连接OC

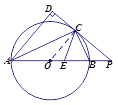
∵PD切⊙O于点C，

∴OC⊥PD．

又∵AD⊥PD，

∴OC∥AD．

∴∠ACO=∠DAC．

又∵OC=OA，

∴∠ACO=∠CAO，

∴∠DAC=∠CAO，

即AC平分∠DAB．

（2）∵AD⊥PD，

∴∠DAC+∠ACD=90°．

又∵AB为⊙O的直径，

∴∠ACB=90°．

∴∠PCB+∠ACD=90°，

∴∠DAC=∠PCB．

又∵∠DAC=∠CAO，

∴∠CAO=∠PCB．

∵CE平分∠ACB，

∴∠ACE=∠BCE，

∴∠CAO+∠ACE=∠PCB+∠BCE，

∴∠PEC=∠PCE，

∴PC=PE，

即△PCE是等腰三角形．