【题目】如图,△ABC为等边三角形,AE=CD,AD交BE于点P,BQ⊥AD于Q.
(1)求证:AD=BE;
(2)设∠BPQ=α,那么α的大小是否随D、E的位置变化而变化?请说明理由;
(3)若PQ=3,PE=1,求AD的长.

参考答案:
【答案】(1)见解析;(2)![]() 的大小不随D、E的位置变化而变化,理由见解析;(3)7
的大小不随D、E的位置变化而变化,理由见解析;(3)7
【解析】
(1)欲证明AD=BE,只要证明△ACD≌△BAE即可.
(2)由α=∠ABE+∠BAP=∠CAD+∠BAP即可得出结论.
(3)在Rt△PBQ中,利用30°角的性质即可知道PB=2PQ,由此可以解决问题.
(1)∵△ABC为等边三角形,
∴AC=AB,∠C=∠BAC=60°
在△ACD和△BAE中,

∴△ACD≌△BAE,
∴AD=BE
(2)不变,理由如下:
由(1)可知:△ACD≌△BAE
∴∠CAD=∠ABE
∵α=∠ABE+∠BAP=∠CAD+∠BAP=60°
故答案为:α的大小不随D、E的位置变化而变化,理由见解析
(3)在△PBQ中,∠PBQ=90°∠BPQ=90°60°=30°
∴BP=2PQ=6
∴AD=BE=BP+PE=6+1=7
故答案为:7
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2-(k+2)x+2k=0.
(1)求证:k取任何实数值,方程总有实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠A的平分线交BC于D. 过C点作CG⊥AB于G,交AD于E. 过D点作DF⊥AB于F. 下列结论:①∠CED=∠CDE;②S△AEC:S△AEG=AC:AG;③∠ADF=2∠FDB;④CE=DF.其中正确的结论有( )
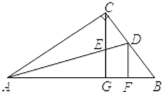
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,CE平分∠ACB,交AB于点E.
(1)求证:AC平分∠DAB;
(2)求证:△PCE是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D在AC上,点F、G分别在AC、BC的延长线上,CE平分∠ACB交BD于点O,且∠EOD+∠OBF=180°,∠F=∠G.则图中与∠ECB相等的角有( )
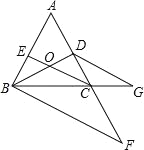
A. 6个 B. 5个 C. 4个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】无锡阳山地区有A、B两村盛产水蜜桃,现A村有水蜜桃200吨,B村有水蜜桃300吨.计划将这些水蜜桃运到C、D两个冷藏仓库,已知C仓库可储存240吨,D仓库可储存260吨;从A村运往C、D两处的费用分别为每吨20元和25元,从B村运往C,D两处的费用分别为每吨15元和18元.设从A村运往C仓库的水蜜桃重量为x吨,A、B两村运往两仓库的水蜜桃运输费用分别为yA元和yB元.
(1)请先填写下表,再根据所填写内容分别求出yA、yB与x之间的函数关系式;
收地运地
C
D
总计
A
x吨
______
200吨
B
______
______
300吨
总计
240吨
260吨
500吨
(2)试讨论A、B两村中,哪个村的运费较少;
(3)考虑到B村的经济承受能力,B村的水蜜桃运费不得超过4830元,在这种情况下,请问怎样调运,才能使两村运费之和最小?求出这个最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向不断地移动,每次移动1个单位长度,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…,那么点A2 019的坐标为________.

相关试题

