【题目】如图,在直角坐标系中,点![]() 是第一象限内的点,直线
是第一象限内的点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,过点
,过点![]() 的直线与
的直线与![]() 轴交于点
轴交于点![]() ,已知直线
,已知直线![]() 上的点的坐标
上的点的坐标![]() 是方程的
是方程的![]() 解,直线
解,直线![]() 上的点的坐标
上的点的坐标![]() 是方程
是方程![]() 的解
的解
(1)求点![]() 的坐标
的坐标
(2)证明:![]() (要求写出每一步的推理依据);
(要求写出每一步的推理依据);
(3)求点![]() 的坐标,并求三角形
的坐标,并求三角形![]() 的面积
的面积

参考答案:
【答案】(1)B(3,4),C(0,4);(2)见解析;(3)点E的坐标为:(1,2),面积为3
【解析】
(1)由直线CD上的点的坐标(x,y)是方程2x+y=4的解,则当x=0时,y=4,则点C的坐标(0,4),由BC⊥y轴,直线AB上的点的坐标(x,y)是方程x-y=-1的解,当y=4时,x=3,则点C的坐标(3,4);
(2)由垂直于同一条直线的两条直线平行得出CB∥x轴,由两平行直线被第三条直线所截,内错角相等得出∠ABC=∠BAD,由对顶角相等得出∠1=∠BAD,等量代换即可得出结论;
(3)由题意得点E的坐标(x,y)是![]() 的解,求出点E的坐标(1,2),再求出点D的坐标(2,0),点A的坐标(-1,0),则AD=3,△AED底边AD上的高为2,由三角形面积公式即可得出结果.
的解,求出点E的坐标(1,2),再求出点D的坐标(2,0),点A的坐标(-1,0),则AD=3,△AED底边AD上的高为2,由三角形面积公式即可得出结果.
(1)解:∵直线CD上的点的坐标(x,y)是方程2x+y=4的解,
∴当x=0时,2×0+y=4,
解得:y=4,
∴点C的坐标为:(0,4),
∵BC⊥y轴,直线AB上的点的坐标(x,y)是方程x-y=-1的解,
∴当y=4时,x-4=-1,
解得:x=3,
∴点B的坐标为:(3,4);
(2)证明:∵BC⊥y轴(已知),
∴CB∥x轴(垂直于同一条直线的两条直线平行),
∵∠ABC=∠BAD(两平行直线被第三条直线所截,内错角相等),
∵∠1=∠BAD(对顶角相等),
∴∠ABC=∠1(等量代换);
(3)解:由题意得点E的坐标(x,y)是![]() 的解,
的解,
解得:![]() ,
,
∴点E的坐标为:(1,2),
∵直线CD上的点的坐标(x,y)是方程2x+y=4的解,
∴当y=0时,2x+0=4,
解得:x=2,
∴点D的坐标为:(2,0),
∵直线AB上的点的坐标(x,y)是方程x-y=-1的解,
∴当y=0时,x-0=-1,
解得:x=-1,
∴点A的坐标为:(-1,0),
∴AD=2-(-1)=3,
∵点E的坐标为:(1,2),
∴△AED底边AD上的高为2,
∴S△ADE=![]() ×3×2=3.
×3×2=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(﹣4,2)、B(n,﹣4)两点是一次函数y=kx+b和反比例函数y=
 图象的两个交点.
图象的两个交点.(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b﹣
 >0的解集.
>0的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,
, ,
, 是
是 的中点,点
的中点,点 在边
在边 上,将
上,将 沿
沿 翻折,使点
翻折,使点 落在点
落在点 处,当
处,当 时,
时, ________.
________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有A、B、C、D四个整数点(即各点均表示整数),且2AB=BC=3CD,若A、D两点表示的数分别为﹣5和6,且AC的中点为E,BD的中点为M,BC之间距点B的距离为
 BC的点N,则该数轴的原点为( )
BC的点N,则该数轴的原点为( )
A. 点E B. 点F C. 点M D. 点N
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=90°,OC为一条射线,OE,OF分别平分∠AOC,∠BOC,那么∠EOF 的度数为_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正整数能表示为两个连续奇数的平方差,那么称这个正整数为“奇特数”.例如:
 ,
, ,
, ;则8、16、24这三个数都是奇特数.
;则8、16、24这三个数都是奇特数.
(1)填空:32___________奇特数,2018_________奇特数.(填“是”或者“不是”)
(2)设两个连续奇数是
 和
和 (其中
(其中 取正整数),由这两个连续奇数构造的奇特数是8的倍数吗?为什么?
取正整数),由这两个连续奇数构造的奇特数是8的倍数吗?为什么?(3)如图所示,拼叠的正方形边长是从1开始的连续奇数…,按此规律拼叠到正方形
 ,其边长为403,求阴影部分的面积.
,其边长为403,求阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 于
于 点,
点, ,点
,点 是
是 边上一点,连接
边上一点,连接 并延长,交
并延长,交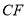 于
于 点,
点, .
.
(1)
 与
与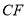 有什么位置关系,说明理由;
有什么位置关系,说明理由;(2)若
 ,
, ,求
,求 的度数和
的度数和 的长度;
的长度;(3)在(2)的条件下,若将
 绕着点
绕着点 顺时针旋转
顺时针旋转 ,则(1)中结论是否仍然成立?如果成立,请证明;如果不成立,请直接写出此时
,则(1)中结论是否仍然成立?如果成立,请证明;如果不成立,请直接写出此时 的度数.
的度数.
相关试题

