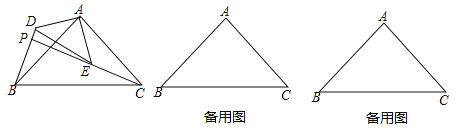
【题目】如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.
(1)求证:BD=CE;
(2)若AB=2,AD=1,把△ADE绕点A旋转,当∠EAC=90°时,求PB的长;
参考答案:
【答案】(1)证明见解析;(2)PB的长为![]() 或
或![]() .
.
【解析】试题分析:(1)依据等腰三角形的性质得到AB=AC,AD=AE,依据同角的余角相等得到∠DAB=∠CAE,然后依据SAS可证明△ADB≌△AEC,最后,依据全等三角形的性质可得到BD=CE;
(2)分为点E在AB上和点E在AB的延长线上两种情况画出图形,然后再证明△PEB∽△AEC,最后依据相似三角形的性质进行证明即可.
试题解析:解:(1)∵△ABC和△ADE是等腰直角三角形,∠BAC=∠DAE=90°,∴AB=AC,AD=AE,∠DAB=∠CAE,∴△ADB≌△AEC,∴BD=CE.
(2)解:①当点E在AB上时,BE=AB﹣AE=1.
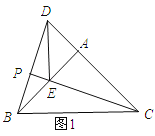
∵∠EAC=90°,∴CE=![]() =
=![]() .
.
同(1)可证△ADB≌△AEC,∴∠DBA=∠ECA.
∵∠PEB=∠AEC,∴△PEB∽△AEC,∴![]() ,∴
,∴![]() ,∴PB=
,∴PB=![]() .
.
②当点E在BA延长线上时,BE=3.
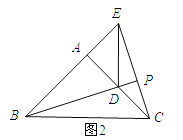
∵∠EAC=90°,∴CE=![]() =
=![]() .
.
同(1)可证△ADB≌△AEC,∴∠DBA=∠ECA.
∵∠BEP=∠CEA,∴△PEB∽△AEC,∴![]() ,∴
,∴![]() ,∴PB=
,∴PB=![]() .
.
综上所述,PB的长为![]() 或
或![]() .
.
-
科目: 来源: 题型:
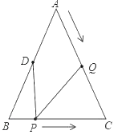
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=12cm,BC=10cm,点D为AB的中点,如果点P在线段BC上以2cm/s的速度由点B向点C运动,同时,点Q在线段AC上由点A向点C 以4cm/s的速度运动.若点P、Q两点分别从点B、A同时出发.
(1)经过2秒后,求证:∠DPQ=∠C.
(2)若△CPQ的周长为18cm,问经过几秒钟后,△CPQ是等腰三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,一次函数
 的图象与反比例函数
的图象与反比例函数 的图象交于
的图象交于 )两点与x轴,y轴分别交于A、B(0,2)两点,如果
)两点与x轴,y轴分别交于A、B(0,2)两点,如果 的面积为6.
的面积为6.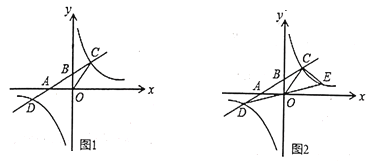
(1)求点A的坐标;
(2)求一次函数和反比例函数的解析式;
(3)如图2,连接DO并延长交反比例函数的图象于点E,连接CE,求点E的坐标和
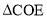 的面积
的面积 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)12+(-3.4)-(-13.4)
(2)
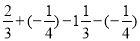
(3)0-5+-25-26
(4)-4÷
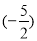 ×
×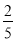
(5)
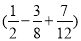 ×(-24)
×(-24) (6)
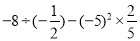
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A.B在数轴上对应的有理数分别是a,b那么A.B之间的距离可以表示为AB=a-b,点P是数轴上一动点,对应数为x,则点P与点A,B的距离分别表示为PA=x-a,PB=x-b,且a+4+
 =0.
=0.(1)直接写出a,b的值;
(2)当
 =2时,求x的值;
=2时,求x的值;(3)当点P在数轴上运动时,是否存在这样的x,使
 ?若存在,请求出的x的值;若不存在,请说明理由。
?若存在,请求出的x的值;若不存在,请说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图四边形ABCD是正方形,点E、F分别在线段BC、DC上,∠BAE=30°.若线段AE绕点A逆时针旋转后与线段AF重合,则旋转的角度是( )

A.30°B.45°C.60°D.90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )

A. AE=CF B. BE=DF C. ∠EBF=∠FDE D. ∠BED=∠BFD
相关试题

