【题目】如图1,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() )两点与x轴,y轴分别交于A、B(0,2)两点,如果
)两点与x轴,y轴分别交于A、B(0,2)两点,如果![]() 的面积为6.
的面积为6.
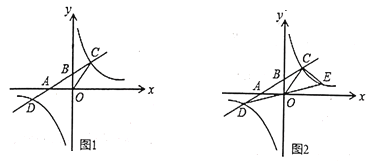
(1)求点A的坐标;
(2)求一次函数和反比例函数的解析式;
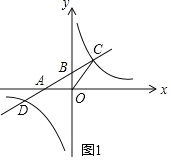
(3)如图2,连接DO并延长交反比例函数的图象于点E,连接CE,求点E的坐标和![]() 的面积
的面积
参考答案:
【答案】(1)A(﹣4,0);(2)![]() ,
,![]() ;(3)
;(3)![]() ,8
,8
【解析】
(1)由三角形面积求出OA=4,即可求得A(-4,0).
(2)利用待定系数法即可求出一次函数的解析式,进而求得C点的坐标,把C点的坐标代入![]() ,求出m的值,得到反比例函数的解析式;
,求出m的值,得到反比例函数的解析式;
(3)先联立两函数解析式得出D点坐标,根据中心对称求得E点的坐标,然后根据三角形的面积公式计算△CED的面积即可.
(1)如图1,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 的面积为6,
的面积为6,
∴![]() ,
,
∵![]() ,
,
∴OA=4,
∴A(﹣4,0);
(2)如图1,把![]() 代入
代入![]() 得
得![]() ,
,
解得![]() ,
,
∴一次函数的解析式为![]() ,
,
把![]() 代入得,
代入得,![]() ,
,
∴![]() ,
,
∵点C在反比例函数![]() 的图象上,
的图象上,
∴m=2×3=6,
∴反比例函数的解析式为![]() ;
;
(3)如图2,作![]() 轴于F,
轴于F,![]() 轴于H,
轴于H,
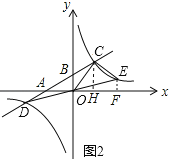
解 ,得
,得![]() ,
,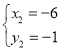 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() =
=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B两点在数轴上,点A表示的数为–10,OB=4OA,点M以每秒2个单位长度的速度从点A开始向左运动,点N以每秒3个单位长度的速度从点B开始向左运动(点M和点N同时出发).

(1)数轴上点B对应的数是__________,线段AB的中点C对应的数是__________;
(2)经过几秒,点M、点N到原点的距离相等?
-
科目: 来源: 题型:
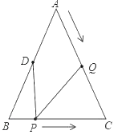
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=12cm,BC=10cm,点D为AB的中点,如果点P在线段BC上以2cm/s的速度由点B向点C运动,同时,点Q在线段AC上由点A向点C 以4cm/s的速度运动.若点P、Q两点分别从点B、A同时出发.
(1)经过2秒后,求证:∠DPQ=∠C.
(2)若△CPQ的周长为18cm,问经过几秒钟后,△CPQ是等腰三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)12+(-3.4)-(-13.4)
(2)
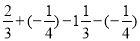
(3)0-5+-25-26
(4)-4÷
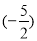 ×
×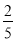
(5)
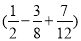 ×(-24)
×(-24) (6)
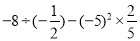
-
科目: 来源: 题型:
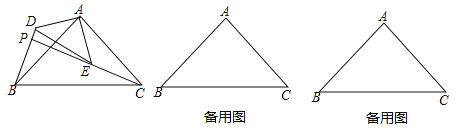
查看答案和解析>>【题目】如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.
(1)求证:BD=CE;
(2)若AB=2,AD=1,把△ADE绕点A旋转,当∠EAC=90°时,求PB的长;
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A.B在数轴上对应的有理数分别是a,b那么A.B之间的距离可以表示为AB=a-b,点P是数轴上一动点,对应数为x,则点P与点A,B的距离分别表示为PA=x-a,PB=x-b,且a+4+
 =0.
=0.(1)直接写出a,b的值;
(2)当
 =2时,求x的值;
=2时,求x的值;(3)当点P在数轴上运动时,是否存在这样的x,使
 ?若存在,请求出的x的值;若不存在,请说明理由。
?若存在,请求出的x的值;若不存在,请说明理由。
相关试题

