【题目】如图,将正方形对折后展开(图④是连续两次对折后再展开),再按图示方法折叠,能够得到一个直角三角形(阴影部分),且它的一条直角边等于斜边的一半,这样的图形有( ).



A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
参考答案:
【答案】C
【解析】
试题根据含30°角所对的直角边等于斜边一半,然后依次判断直角三角形中能否找到一个角等于30°,从而判断出答案.
试题解析:设正方形的边长为a,
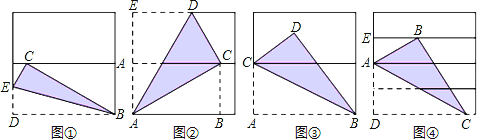
在图①中,CE=ED=![]() a,BC=DB=a,
a,BC=DB=a,
故∠EBC=∠CEB≠30°,故△ECB,故不能满足它的一条直角边等于斜边的一半.
在图②中,BC=![]() a,AC=AE=a,
a,AC=AE=a,
故∠BAC=30°,
从而可得∠CAD=∠EAD=30°,故能满足它的一条直角边等于斜边的一半.
在图③中,AC=![]() a,AB=a,
a,AB=a,
故∠ABC=∠DBC≠30°,故不能满足它的一条直角边等于斜边的一半.
在图④中,AE=![]() a,AB=AD=
a,AB=AD=![]() a,
a,
故∠ABE=30°,∠EAB=60°,
从而可得∠BAC=∠DAC=60°,∠ACB=30°,故能满足它的一条直角边等于斜边的一半.
综上可得有2个满足条件.
故选C.
-
科目: 来源: 题型:
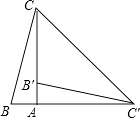
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′,连接CC′.若∠CC′B′=32°,则∠B的大小是( )
A.32°
B.64°
C.77°
D.87° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=(x+m)2﹣n的图象如图所示,则一次函数y=mx+n与反比例函数y=
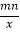 的图象可能是( )
的图象可能是( )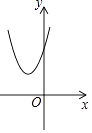
A.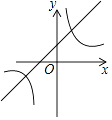
B.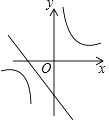
C.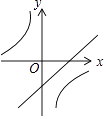
D.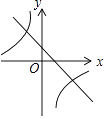
-
科目: 来源: 题型:
查看答案和解析>>【题目】某快递公司针对新客户优惠收费,首件物品的收费标准为:若重量不超过10千克,则免运费;当重量为
 千克时,运费为
千克时,运费为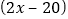 元;第二件物品的收费标准为:当重量为
元;第二件物品的收费标准为:当重量为 千克时,运费为
千克时,运费为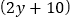 元。
元。(1)若新客户所奇首件物品的重量为13千克,则运费是多少元?
(2)若新客户所寄首件物品的运费为32元,则物品的重量是多少千克?
(3)若新客户所寄首件物品与第二件物品的重量之比为2:5,共付运费为60元,则两件物品的重量各是多少千克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=2x+4
(1)在如图所示的平面直角坐标系中,画出函数的图象;

2)求图象与x轴的交点A的坐标,与y轴交点B的坐标;
(3)在(2)的条件下,求出△AOB的面积;
(4)利用图象直接写出:当y<0时,x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D、E、F分别为BC、AD、BE的中点,若△BFD的面积为6,则 △ABC的面积等于_____________.
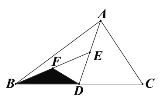
-
科目: 来源: 题型:
查看答案和解析>>【题目】小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16min到家,再过5min小东到达学校,小东始终以100m/min的速度步行,小东和妈妈的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示,下列四种说法:

①打电话时,小东和妈妈的距离为1400米;
②小东和妈妈相遇后,妈妈回家速度为50m/min;
③小东打完电话后,经过27min到达学校;
④小东家离学校的距离为2900m.
其中正确的个数是( )
A.1个
B.2个
C.3个
D.4个
相关试题

