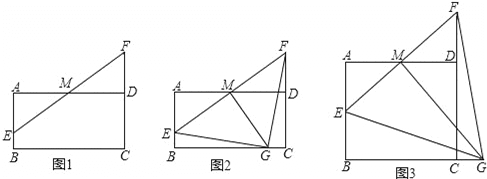
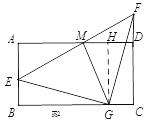
【题目】如图,在矩形ABCD中,AD=4,M是AD的中点,点E是线段AB上一动点,连结EM并延长交线段CD的延长线于点F.
(1)如图1,求证:AE=DF;
(2)如图2,若AB=2,过点M作MG⊥EF交线段BC于点G,求证:△GEF是等腰直角三角形;
(3)如图3,若AB=2![]() ,过点M作MG⊥EF交线段BC的延长线于点G.求线段AE长度的取值范围.
,过点M作MG⊥EF交线段BC的延长线于点G.求线段AE长度的取值范围.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3 )![]() <AE≤2
<AE≤2![]() .
.
【解析】试题分析:(1)根据矩形的性质得到∠EAM=∠FDM=90°,根据全等三角形的判定定理得到△AEM≌△DFM(ASA),由全等三角形的性质即可得到结论;
(2)过点G作GH⊥AD于H,推出四边ABGH为矩形,得到∠AME+∠AEM=90°,由于∠AME+∠GMH=90°等量代换得到∠AEM=∠GMH,推出△AEM≌△HMG(AAS),根据全等三角形的性质得到ME=MG,求得∠EGM=45°.根据全等三角形的性质得到ME=MF.即可得到结论;
(3 )根据四边形ABCD是矩形,得到∠A=∠ADC=90°,等量代换得到∠AEM=∠DMC,根据相似三角形的性质得到![]() ,代入数据求得AE=
,代入数据求得AE=![]() ,当E、B重合时,AE最长为2
,当E、B重合时,AE最长为2![]() ,于是得到结论.
,于是得到结论.
试题解析:(1)如图1,在矩形ABCD中,∠EAM=∠FDM=90°,
∵M是AD的中点,∴AM=DM,又∠AME=∠FMD,
在△AEM与△DFM中, 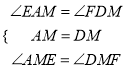 ,
,
∴△AEM≌△DFM(ASA),
∴AE=DF;
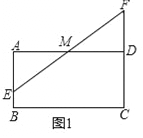
(2)如图2,过点G作GH⊥AD于H,
∴∠A=∠B=∠AHG=90°,∴四边ABGH为矩形,∴∠AME+∠AEM=90°,
∵MG⊥EF,∴∠GME=90°.∴∠AME+∠GMH=90°∴∠AEM=∠GMH,
∵AD=4,M是AD的中点,∴AM=2,
∵四边ABGH为矩形,∴AB=HG=2,∴AM=HG,
在△AEM与△HMG中, 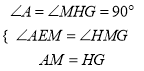 ,
,
∴△AEM≌△HMG(AAS),∴ME=MG,∴∠EGM=45°.
由(1)得△AEM≌△DFM,∴ME=MF.
∵MG⊥EF,∴GE=GF,∴∠EGF=2∠EGM=90°.
∴△GEF是等腰直角三角形;
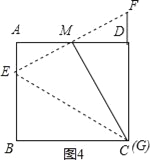
(3 )当C、G重合时,如图4,
∵四边形ABCD是矩形,∴∠A=∠ADC=90°,∴∠AME+∠AEM=90°.
∵MG⊥EF,∴∠EMG=90°,∴∠AME+∠DMC=90°,∴∠AEM=∠DMC,
∴△AEM∽△DMC∴![]() ,∴
,∴![]() ,∴AE=
,∴AE=![]() ,
,
当E、B重合时,AE最长为2![]() ,
,
∴![]() <AE≤2
<AE≤2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A,B两数的平均数是16,B,C两数的平均数是21,那么C-A=__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将点P(-3,4)先向下平移3个单位,再向右平移2个单位后得到点Q,则点Q的坐标是______.
-
科目: 来源: 题型:
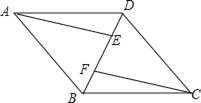
查看答案和解析>>【题目】已知:如图,四边形ABCD是平行四边形,AE∥CF,且分别交对角线BD于点E,F.
(1)求证:△AEB≌△CFD;
(2)连接AF,CE,若∠AFE=∠CFE,求证:四边形AFCE是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,点A(0,4),B(3,0),以AB为边在第一象限内作正方形ABCD,直线L:y=kx+3.
(1)当直线l经过D点时,求点D的坐标及k的值;
(2)当直线L与正方形有两个交点时,直接写出k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=x2+bx+c经过A(﹣1,0),B(3,0)两点,与y轴相交于点C,该抛物线的顶点为点D.
(1)求该抛物线的解析式及点D的坐标;
(2)连接AC,CD,BD,BC,设△AOC、△BOC、△BCD的面积分别为S1,S2和S3,求证:S3=
 ;
;(3)点M是线段AB上一动点(不包括点A和点B),过点M作MN∥BC交AC于点N,连接MC,是否存在点M使∠AMN=∠ACM?若存在,求出点M的坐标和此时直线MN的解析式;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】运用等式性质进行的变形,不正确的是( )
A.如果a=b,那么a﹣c=b﹣c
B.如果a=b,那么a+c=b+c
C.如果a=b,那么ac=bc
D.如果ac=bc,那么a=b
相关试题

