【题目】已知:如图①,在矩形ABCD中,AB=5,AD=.E为矩形外一点,且△EBA∽△ABD.
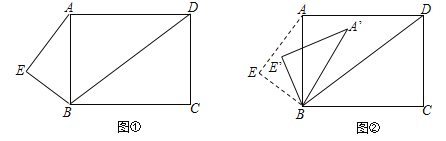
(1)、求AE和BE的长;
(2)、若将△ABE沿着射线BD方向平移,设平移的距离为m(平移距离指点B沿BD方向所经过的线段长度).当点E分别平移到线段AB、AD上时,直接写出相应的m的值;
(3)、如图②,将△ABE绕点B顺时针旋转一个角α(0°<α<180°),记旋转中的△ABE为△A′BE′,在旋转过程中,设A′E′所在的直线与直线AD交于点P,与直线BD交于点Q.是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时DQ的长;若不存在,请说明理由.
参考答案:
【答案】(1)、AE=4,BE=3;(2)、m=3;m=![]() ;(3)、DQ=3
;(3)、DQ=3![]() -
-![]() 、
、![]() 、
、![]() -
-![]() 或
或![]() .
.
【解析】
试题分析:(1)、根据三角形相似得出AE和BE的长度;(2)、分两种情况分别计算出m的值;(3)、分四种情况分别求出DQ的长度.
试题解析:(1)、AE=4,BE=3
(2)、点E在AB上时,m=3;点E在AD上时,m=![]()
(3)、存在.理由如下:在旋转过程中,等腰△DPQ依次有以下4种情形:
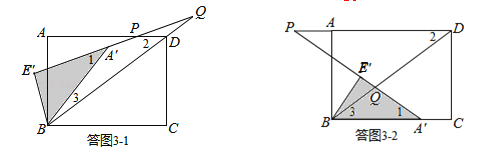
①如图3﹣1所示,点Q落在BD延长线上,且PD=DQ,求得DQ=3![]() -
-![]() ;
;
②如图3﹣2所示,点Q落在BD上,且PQ=DQ,求得DQ=![]() ;
;
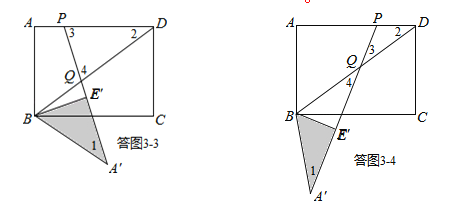
③如图3﹣3所示,点Q落在BD上,且PD=DQ,求得DQ=![]() -
-![]() ;
;
④如图3﹣4所示,点Q落在BD上,且PQ=PD,求得DQ=![]() .
.
综上所述,存在4组符合条件的点P、点Q,使△DPQ为等腰三角形:
DQ的长度分别为3![]() -
-![]() 、
、![]() 、
、![]() -
-![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】要建一个面积为150平方米的长方形养鸡场,为了节约材料,鸡场一边靠着原有的一堵墙,墙长为18米,另三边用篱笆围成,如篱笆长度为35米,且要求用完。求鸡场的长与宽各是多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE=
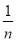 AD (n为大于2的整数),连接BE,作BE的垂直平分线分别交AD,BC于点F,G,FG与BE的交点为O,连接BF和EG.
AD (n为大于2的整数),连接BE,作BE的垂直平分线分别交AD,BC于点F,G,FG与BE的交点为O,连接BF和EG.(1)试判断四边形BFEG的形状,并说明理由;
(2)当AB=a(a为常数),n=3时,求FG的长;
(3)记四边形BFEG的面积为S1,矩形ABCD的面积为S2,当
 时,求n的值.(直接写出结果,不必写出解答过程)
时,求n的值.(直接写出结果,不必写出解答过程)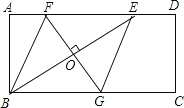
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利44元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出5件。若商场平均每天要盈利1600元,每件衬衫应降价多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=1是方程2x2﹣3x﹣m=0的一个根,则m的值为( )
A.1
B.5
C.-1
D.-5 -
科目: 来源: 题型:
查看答案和解析>>【题目】某码头上有20名工人装载一批货物,已知每人往一艘轮船上装载2吨货物,装载完毕恰好用了6天,轮船到达目的地后,另一批工人开始卸货,计划平均每天卸货v吨,刚要卸货时遇到紧急情况,要求船上的货物卸载完毕不超过4天,则这批工人实际每天至少应卸货( )
A.30吨
B.40吨
C.50吨
D.60吨 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列问题中,两个变量成正比例的是( )
A.等腰三角形的面积一定,它的底边和底边上的高
B.等边三角形的面积和它的边长
C.长方形的一边长确定,它的周长与另一边长
D.长方形的一边长确定,它的面积与另一边长
相关试题

