搜索
【题目】要建一个面积为150平方米的长方形养鸡场，为了节约材料，鸡场一边靠着原有的一堵墙，墙长为18米，另三边用篱笆围成，如篱笆长度为35米，且要求用完。求鸡场的长与宽各是多少米？
参考答案：
【答案】与墙垂直的一边长为10m,与墙平行的边长为15m.
【解析】
试题分析：设围在两边的是
m，则只围了一边的是（35-2
）m，x和（35-2）就是鸡场的长或宽．然后用面积做等量关系可列方程求解，同时对两根要进行检验是否符合实际情况。
试题解析：设与墙垂直的一边长为m，则与墙平行的边长为（35-2）m，可列方程为
即
解得
当=10时，35-2=15
当=7.5时，35-2=20＞18(舍去)
所以鸡场的面积能达到
，方案是与墙垂直的一边长为10m,与墙平行的边长为15m.
-
科目： 来源： 题型：
查看答案和解析>>【题目】若y关于x的函数y=（m-2）x+n是正比例函数，则m，n应满足的条件是（ ）
A.m≠2且n=0
B.m=2且n=0
C.m≠2
D.n=0 -
科目： 来源： 题型：
查看答案和解析>>【题目】某公司去年1~ 3月平均每月盈利2万元，4~6月平均每月亏损1.5万元，7~10月平均每月亏损1.2万元，11~12月平均每月盈利3.4万元，该公司总的盈、亏情况如何？（假设盈利为正，亏损为负）
-
科目： 来源： 题型：
查看答案和解析>>【题目】电影院的座位排列时，后一排总比前一排高，并且每一横排呈圆弧形，这是为了____________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形ABCD中，AD=2AB，E是AD边上一点，DE=
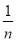AD (n为大于2的整数)，连接BE，作BE的垂直平分线分别交AD，BC于点F，G，FG与BE的交点为O，连接BF和EG．(1)试判断四边形BFEG的形状，并说明理由；
(2)当AB=a(a为常数)，n=3时，求FG的长；
(3)记四边形BFEG的面积为S1，矩形ABCD的面积为S2，当
时，求n的值．(直接写出结果，不必写出解答过程)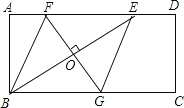
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利44元，为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出5件。若商场平均每天要盈利1600元，每件衬衫应降价多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图①，在矩形ABCD中，AB＝5，AD＝．E为矩形外一点，且△EBA∽△ABD．
(1)、求AE和BE的长；
(2)、若将△ABE沿着射线BD方向平移，设平移的距离为m（平移距离指点B沿BD方向所经过的线段长度）．当点E分别平移到线段AB、AD上时，直接写出相应的m的值；
(3)、如图②，将△ABE绕点B顺时针旋转一个角α（0°＜α＜180°），记旋转中的△ABE为△A′BE′，在旋转过程中，设A′E′所在的直线与直线AD交于点P，与直线BD交于点Q．是否存在这样的P、Q两点，使△DPQ为等腰三角形？若存在，求出此时DQ的长；若不存在，请说明理由．
相关试题
