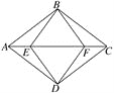
【题目】如图,ABCD是平行四边形,E、F是对角线AC上的两点,若∠ABF=∠CDE=90°.
(1)求证:四边形BEDF是平行四边形;
(2)若AB=AD=8,BF=6,求AE的长.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)由平行四边形的性质得出AB=CD,AB∥CD,证出∠BAC=∠DCA,由ASA证明△ABF≌△CDE,得出BF=DE,∠AFB=∠CED,证出BF∥DE,即可得出结论;
(2)连接BD交AC于G,证明四边形ABCD是菱形,得出AC⊥BD,证出四边形BEDF是菱形,得出BE=BF=6,由勾股定理求出AF,由三角形的面积关系求出BG,再由勾股定理求出EG,即可得出结果.
(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAC=∠DCA,
在△ABF和△CDE中,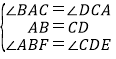 ,
,
∴△ABF≌△CDE(ASA),
∴BF=DE,∠AFB=∠CED,
∴BF∥DE,
∴四边形BEDF是平行四边形;
(2)连接BD交AC于G,如图所示:
∵AB=AD,
∴四边形ABCD是菱形,
∴AC⊥BD,
∴四边形BEDF是菱形,
∴BE=BF=6,EG=FG,
∵∠ABF=90°,AB=AD=8,BF=6,
∴AF=![]() =10,
=10,
∵△ABF的面积=![]() AF·BG=
AF·BG=![]() AB×BF,
AB×BF,
∴BG=![]() =
=![]() ,
,
∴EG=![]() =
=![]() ,
,
∴AE=AF-2EG=10-2×![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国淡水资源短缺问题十分突出,已成为我国经济和社会可持续发展的重要制约因素,节约用水是各地的一件大事.某校初三学生为了调查居民用水情况,随机抽查了某小区20户家庭的月用水量,结果如表所示:

(1)求这20户家庭月用水量的平均数、众数及中位数.
(2)政府为了鼓励节约用水,拟试行水价浮动政策.即设定每个家庭月基本用水量a(t),家庭月用水量不超过a(t)的部分按原价收费,超过a(t)的部分加倍收费.
①你认为以平均数作为该小区的家庭月基本用水量a(t)合理吗?为什么?(简述理由)
②你认为该小区的家庭月基本用水量a(t)为多少时较为合理?为什么?(简述理由)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,D是边BC上一动点(不与B,C重合),DE⊥AB于点E,点F是线段AD的中点,连接EF,CF.
(1)试猜想线段EF与CF的大小关系,并加以证明.
(2)若∠BAC=30°,连接CE,在D点运动过程中,探求CE与AD的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O直径,AC为⊙O的弦,过⊙O外的点D作DE⊥OA于点E,交AC于点F,连接DC并延长交AB的延长线于点P,且∠D=2∠A,作CH⊥AB于点H.

(1)判断直线DC与⊙O的位置关系,并说明理由;
(2)若HB=2,cosD=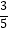 ,请求出AC的长.
,请求出AC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场对某种商品进行销售,第x天的销售单价为m元/件,日销售量为n件,其中m,n分别是x(1≤x≤30,且x为整数)的一次函数,销售情况如表:
销售第x天
第1天
第2天
第3天
第4天
…
第30天
销售单价m(元/件)
49
48
47
46
…
20
日销售量n(件)
45
50
55
60
…
190
(1)观察表中数据,分别直接写出m与x,n与x的函数关系式: , ;
(2)求商场销售该商品第几天时该商品的日销售额恰好为3600元?
(3)销售商品的第15天为儿童节,请问:在儿童节前(不包括儿童节当天)销售该商品第几天时该商品的日销售额最多?商场决定将这天该商品的日销售额捐献给儿童福利院,试求出商场可捐款多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】某地区教育部门要了解初中学生阅读课外书籍的情况,随机调查了本地区500名初中学生一学期阅读课外书的本数,并绘制了如下的统计图,请根据统计图反映的信息回答问题.
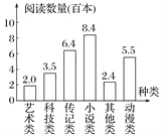
(1)这些课外书籍中,哪类书的阅读数量最大?
(2)这500名学生一学期平均每人阅读课外书多少本?(精确到1本)
(3)若该地区共有2万名初中学生,请估计他们一学期阅读课外书的总本数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在△
 中,
中,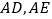 分别是△
分别是△ 的高和角平分线,若
的高和角平分线,若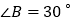 ,
,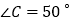 ;求
;求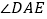 的度数.
的度数.
相关试题

