【题目】如图,在Rt△ABC中,∠ACB=90°,D是边BC上一动点(不与B,C重合),DE⊥AB于点E,点F是线段AD的中点,连接EF,CF.
(1)试猜想线段EF与CF的大小关系,并加以证明.
(2)若∠BAC=30°,连接CE,在D点运动过程中,探求CE与AD的数量关系.

参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)EF和CF分别是直角△AED和直角△ACD斜边上的中线,依据直角三角形斜边上的中线等于斜边的一半即可证得;
(2)证明△EFC是等边三角形,然后根据等边三角形的定义以及直角三角形的性质求解.
(1)EF=CF,理由如下:
在Rt△AED和Rt△ACD中,
∵点F是线段AD的中点,
∴EF=![]() AD,CF=
AD,CF=![]() AD,
AD,
∴EF=CF;
(2)由(1)可知,EF=AF=CF,
∴∠AEF=∠EAF,∠ACF=∠CAF,
∴∠EFD=2∠EAF,∠CFD=2∠CAF,
∴∠EFC=2∠BAC=60°,
又EF=CF,
∴△EFC为等边三角形,
∴CE=EF=![]() AD.
AD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我校50名学生在某一天调查了75户家庭丢弃塑料袋的情况,统计结果如下表:

根据上表回答下列问题:
(1)这天,一个家庭一天最多丢弃________个塑料袋.
(2)这天,丢弃3个塑料袋的家庭户数占总户数的________.
(3)该校所在的居民区共有居民0.8万户,则该区一天丢弃的塑料袋有多少个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点D,E分别是△ABC的边AB,AC的中点.
(1)如图1,点O是△ABC内的动点,点O,F分别是OB,OC的中点,求证:DEFG是平行四边形;
(2)如图2,若BE交DC于点O,请问AO的延长线经过BC的中点吗?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】我国淡水资源短缺问题十分突出,已成为我国经济和社会可持续发展的重要制约因素,节约用水是各地的一件大事.某校初三学生为了调查居民用水情况,随机抽查了某小区20户家庭的月用水量,结果如表所示:

(1)求这20户家庭月用水量的平均数、众数及中位数.
(2)政府为了鼓励节约用水,拟试行水价浮动政策.即设定每个家庭月基本用水量a(t),家庭月用水量不超过a(t)的部分按原价收费,超过a(t)的部分加倍收费.
①你认为以平均数作为该小区的家庭月基本用水量a(t)合理吗?为什么?(简述理由)
②你认为该小区的家庭月基本用水量a(t)为多少时较为合理?为什么?(简述理由)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O直径,AC为⊙O的弦,过⊙O外的点D作DE⊥OA于点E,交AC于点F,连接DC并延长交AB的延长线于点P,且∠D=2∠A,作CH⊥AB于点H.

(1)判断直线DC与⊙O的位置关系,并说明理由;
(2)若HB=2,cosD=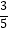 ,请求出AC的长.
,请求出AC的长. -
科目: 来源: 题型:
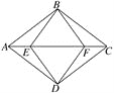
查看答案和解析>>【题目】如图,ABCD是平行四边形,E、F是对角线AC上的两点,若∠ABF=∠CDE=90°.
(1)求证:四边形BEDF是平行四边形;
(2)若AB=AD=8,BF=6,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场对某种商品进行销售,第x天的销售单价为m元/件,日销售量为n件,其中m,n分别是x(1≤x≤30,且x为整数)的一次函数,销售情况如表:
销售第x天
第1天
第2天
第3天
第4天
…
第30天
销售单价m(元/件)
49
48
47
46
…
20
日销售量n(件)
45
50
55
60
…
190
(1)观察表中数据,分别直接写出m与x,n与x的函数关系式: , ;
(2)求商场销售该商品第几天时该商品的日销售额恰好为3600元?
(3)销售商品的第15天为儿童节,请问:在儿童节前(不包括儿童节当天)销售该商品第几天时该商品的日销售额最多?商场决定将这天该商品的日销售额捐献给儿童福利院,试求出商场可捐款多少元?
相关试题

