【题目】若两个二次函数图像的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”.
(1)请写出两个为“同簇二次函数”的函数;
(2)已知关于x的二次函数y1=2x2-4mx+2m2+1和y2=ax2+bx+5,其中y1的图像经过点A(1,1),若y1+y2与y1为“同簇二次函数”,求函数y2的表达式,并求出当
2≤x≤3时,y2的最小值.
参考答案:
【答案】
(1)解:由“同族二次函数的定义”可知: ![]() 和
和 ![]() 是一对“同族二次函数”(答案不唯一);
是一对“同族二次函数”(答案不唯一);
(2)解:∵ ![]() 的图象过点A(1,1),
的图象过点A(1,1),
∴ ![]() ,解得:
,解得: ![]() ,
,
∴ ![]() ,
,
∴ ![]() 的顶点坐标为(1,1),且
的顶点坐标为(1,1),且 ![]() ,
,
∵ ![]() 与
与 ![]() 是“同族二次函数”,
是“同族二次函数”,
∴ ![]() 的顶点坐标也为(1,1),
的顶点坐标也为(1,1),
∴ 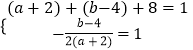 ,解得:
,解得: ![]() ,
,
∴ ![]() ,
,
又∵ ![]() 在对称轴
在对称轴 ![]() 的右侧,
的右侧,
∴当 ![]() 时,
时, ![]() 2最小=5.
2最小=5.
【解析】(1)在写函数式时,抓住若两个二次函数图像的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”,即可写出函数解析式。
(2)先将点A的坐标代入y1求出y1的函数解析式,再求出y1的顶点坐标,求出y1+y2与x的函数解析式,再将(1,1)代入y1+y2与x的函数解析式,建立方程,再根据对称轴x=1建立方程,求出a、b的值,即可写出 y 2 与x的函数解析式,再根据2 ≤ x ≤ 3及二次函数的增减性求出y2的最小值.。
【考点精析】关于本题考查的二次函数的性质,需要了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中,小正方形的边长为1,△ABC的顶点在格点上.
(1)判断△ABC是否是直角三角形?并说明理由.
(2)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC , OD与AC交于点E.
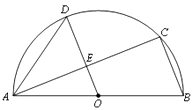
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长. -
科目: 来源: 题型:
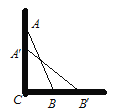
查看答案和解析>>【题目】一架长2.5米的梯子AB如图所示斜靠在一面墙上,这时梯足B离墙底C(∠C=90°)的距离BC为0.7米.
(1)求此时梯顶A距地面的高度AC;
(2)如果梯顶A下滑0.9米,那么梯足B在水平方向,向右滑动了多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=Rt∠,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.

(1)出发2秒后,求△ABP的周长.
(2)问t满足什么条件时,△BCP为直角三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在四边形ABCD中,∠A=90°,AB=3,AD=4,BC=12,CD=13,求四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】初中生在数学运算中使用计算器的现象越来越普遍,某校一兴趣小组随机抽查了本校若干名学生使用计算器的情况.以下是根据抽查结果绘制出的不完整的条形统计图和扇形统计图:
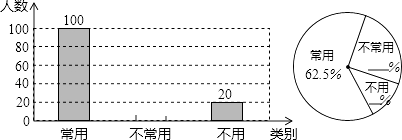
请根据上述统计图提供的信息,完成下列问题:
(1)这次抽查的样本容量是;
(2)请补全上述条形统计图和扇形统计图;
(3)若从这次接受调查的学生中,随机抽查一名学生恰好是“不常用”计算器的概率是多少?
相关试题

