【题目】已知在四边形ABCD中,∠A=90°,AB=3,AD=4,BC=12,CD=13,求四边形ABCD的面积.

参考答案:
【答案】36
【解析】
试题根据勾股定理求得BD=5;由勾股定理的逆定理判定△BCD为直角三角形,则四边形ABCD的面积=△ABD的面积+△BCD的面积.
试题解析:∵在△ABD中,∠A是直角,AB=3,AD=4,
∴由勾股定理得 BD2=AD2+AB2=25.则BD=5,
又∵在△BCD中,BC=12,DC=13,
∴CD2=BD2+BC2=169,
∴△BCD为直角三角形,且∠DBC=90°,
∴S四边形ABCD=S△ABD+S△BCD=![]() ADAB+
ADAB+![]() BDBC=
BDBC=![]() ×4×3+
×4×3+![]() ×5×12=36.
×5×12=36.
即四边形ABCD的面积是36.
考点: 1.勾股定理;2.勾股定理的逆定理.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,折叠长方形一边AD,点D落在BC边的点F处, 已知BC=10厘米,AB=8厘米,求FC和EF的长.
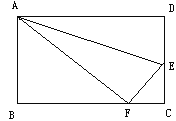
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,∠BAC=2∠DAE=2α.
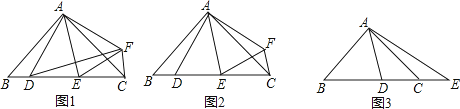
(1)如图1,若点D关于直线AE的对称点为F,求证:△ADF∽△ABC;
(2)如图2,在(1)的条件下,若α=45°,求证:DE2=BD2+CE2;
(3)如图3,若α=45°,点E在BC的延长线上,则等式DE2=BD2+CE2还能成立吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,已知:点A(﹣2,﹣1)在双曲线C:y=
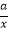 上,直线l1:y=﹣x+2,直线l2与l1关于原点成中心对称,F1(2,2),F2(﹣2,﹣2)两点间的连线与曲线C在第一象限内的交点为B,P是曲线C上第一象限内异于B的一动点,过P作x轴平行线分别交l1 , l2于M,N两点.
上,直线l1:y=﹣x+2,直线l2与l1关于原点成中心对称,F1(2,2),F2(﹣2,﹣2)两点间的连线与曲线C在第一象限内的交点为B,P是曲线C上第一象限内异于B的一动点,过P作x轴平行线分别交l1 , l2于M,N两点.
(1)求双曲线C及直线l2的解析式;
(2)求证:PF2﹣PF1=MN=4;
(3)如图2所示,△PF1F2的内切圆与F1F2 , PF1 , PF2三边分别相切于点Q,R,S,求证:点Q与点B重合.(参考公式:在平面坐标系中,若有点A(x1 , y1),B(x2 , y2),则A、B两点间的距离公式为AB=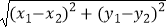 .)
.) -
科目: 来源: 题型:
查看答案和解析>>【题目】求下列各式的值:
(1)
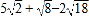 (2)
(2)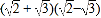
(3)
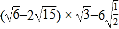 (4)
(4)
(5)
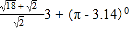 +
+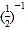 (6)
(6) 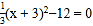
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从①∠1=∠2 ②∠C=∠D ③∠A=∠F 三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )
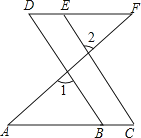
A.0
B.1
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】以下列数组作为三角形的三条边长,其中能构成直角三角形的是( )
A. 1,
 ,3 B.
,3 B.  ,
,  ,5 C. 1.5,2,2.5 D.
,5 C. 1.5,2,2.5 D. 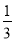 ,
,  ,
, 
【答案】C
【解析】A、12+(
 )2≠32,不能构成直角三角形,故选项错误;
)2≠32,不能构成直角三角形,故选项错误;B、(
 2+(
2+( )2≠52,不能构成直角三角形,故选项错误;
)2≠52,不能构成直角三角形,故选项错误;C、1.52+22=2.52,能构成直角三角形,故选项正确;
D、(
 ))2+(
))2+( )2≠(
)2≠( )2,不能构成直角三角形,故选项错误.
)2,不能构成直角三角形,故选项错误.故选:C.
【题型】单选题
【结束】
3【题目】在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到斜边AB的距离是( )
(A)
 (B)
(B) (C)9 (D)6
(C)9 (D)6
相关试题

