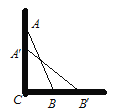
【题目】一架长2.5米的梯子AB如图所示斜靠在一面墙上,这时梯足B离墙底C(∠C=90°)的距离BC为0.7米.
(1)求此时梯顶A距地面的高度AC;
(2)如果梯顶A下滑0.9米,那么梯足B在水平方向,向右滑动了多少米?
参考答案:
【答案】(1)2.4m;(2)1.3m.
【解析】试题分析:(1)在直角三角形ABC中,利用勾股定理即可求出AC的长;
(2)首先求出AC的长,利用勾股定理可求出B′C的长,进而得到BB′=CB′-CB的值.
试题解析:(1)在Rt△ABC中,由勾股定理,得AC2+BC2=AB2,
∴AC2+0.72=2.52,
解得AC=2.4(m),
答:此时梯顶距地面的高度AC为2.4m;
(2)由题意得:A′C=2.4-0.9=1.5,A′B′=2.5,
在Rt△A′B′C中,由勾股定理得A′C2+B′C2=A′B′2,
∴1.52+B′C2=2.52.
解得B′C =2(m),
∴BB′= B′C-BC=2-0.7=1.3(m),
答:梯足在水平方向向右滑动了1.3m.
-
科目: 来源: 题型:
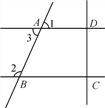
查看答案和解析>>【题目】如图所示,已知AD∥BC,且DC⊥AD于D.
(1)DC与BC有怎样的位置关系?说说你的理由;
(2)你能说明∠1+∠2=180°吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中,小正方形的边长为1,△ABC的顶点在格点上.
(1)判断△ABC是否是直角三角形?并说明理由.
(2)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC , OD与AC交于点E.
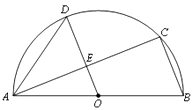
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】若两个二次函数图像的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”.
(1)请写出两个为“同簇二次函数”的函数;
(2)已知关于x的二次函数y1=2x2-4mx+2m2+1和y2=ax2+bx+5,其中y1的图像经过点A(1,1),若y1+y2与y1为“同簇二次函数”,求函数y2的表达式,并求出当
2≤x≤3时,y2的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=Rt∠,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.

(1)出发2秒后,求△ABP的周长.
(2)问t满足什么条件时,△BCP为直角三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在四边形ABCD中,∠A=90°,AB=3,AD=4,BC=12,CD=13,求四边形ABCD的面积.

相关试题

