【题目】如图,△ABC是等边三角形,AD是角平分线,△ADE是等边三角形,下列结论:①AD⊥BC;②EF=FD;③BE=BD.其中正确结论的个数为( )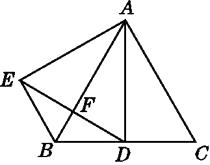
A.3
B.2
C.1
D.0
参考答案:
【答案】A
【解析】∵△ABC是等边三角形,
∴AB=AC,
又∵AD是∠BAC的平分线,
∴AD⊥BC,BD=DC,
∵△ABC和△ADE是等边三角形,
∴AE=AD,AB=AC,∠EAD=∠BAC=60°,
∴∠EAD-∠BAD=∠BAC-∠BAD,
∴∠BAE=∠DAC,
在△BAE和△CAD中,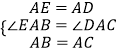
∴△BAE≌△CAD(SAS),
∴∠DAC=∠BAE,BE=DC,
又∵BD=DC,
∴BE=BD,
∵△ABC是等边三角形,
∴∠BAC=60°,
∵AD是∠BAC的平分线,
∴∠DAC=30°,
∴∠BAE=30°,
∵△ADE是等边三角形,
∴∠DAE=60°,
∴∠BAD=30°=∠BAE,
∵AE=AD,
∴EF=DF(三线合一),
即①②③都符合题意。
故应选:A 。
【考点精析】关于本题考查的等腰三角形的性质和等边三角形的性质,需要了解等腰三角形的两个底角相等(简称:等边对等角);等边三角形的三个角都相等并且每个角都是60°才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】教室里,第6列第3个座位记作(6,3),则第3列第5个座位记作_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
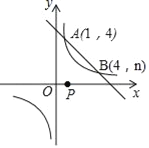
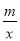 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.(1)求反比例函数的解析式;
(2)求一次函数的解析式;
(3)点P是x轴上的一动点,当PA+PB最小时,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知菱形ABCD的边长为1,∠DAB=60°,E为AD上的动点,F在CD上,且AE+CF=1,
设△BEF的面积为y,AE=x,当点E运动时,能正确描述y与x关系的图像是( )

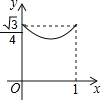
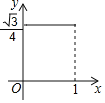
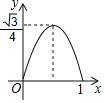
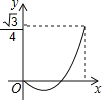
A. B. C. D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x(x+4)=﹣3(x+4)的解是 .
-
科目: 来源: 题型:
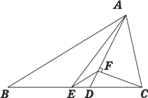
查看答案和解析>>【题目】如图,△ABC中,AB=12,AC=5,AD是∠BAC角平分线,AE是BC边上的中线,
过点C做CF⊥AD于F,连接EF,则线段EF的长为_______.
-
科目: 来源: 题型:
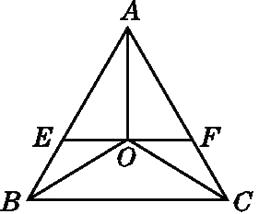
查看答案和解析>>【题目】如图,等边三角形ABC的三条角平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,那么这个图形中的等腰三角形共有( )
A.4个
B.5个
C.6个
D.7个
相关试题

